Daten – oder Zahlen, die die Welt bedeuten
Wir haben jetzt einen groben Einblick in die Grundideen von Software und den Systemen, auf denen sie laufen soll. Was uns jetzt
noch fehlt ist, wie wir eigentlich Daten in unserem Speicher ablegen können. Bis jetzt sind es ja nur Zahlen, welche aus der
mathematischen Zahlenmenge der Natürlichen Zahlen N0 entstammen und je nach Anzahl der zur
Verfügung stehenden Bits nach oben begrenzt sind. Wir wollen aber viel mehr abbilden. Beispielsweise möchten wir gerne
negative Zahlen nutzen, Zahlen mit Nachkommanstellen und auch Daten außerhalb des Zahlenbereiches wie Schriftzeichen.
Wir brauchen also Konzepte, wie wir unsere Bitfolgen im Speicher nicht nur 1:1 in Dezimalzahlen umwandeln und
umgekehrt, sondern wie wir sie auch anderweitig interpretieren können, so dass andere Anwendungsfälle möglich sind.

Zweierkomplement
Beginnen wir mit der Definition von negativen Werten. Wenn wir naiv vorgehen würden, dann könnten wir einfach bei
einer 16 Bit Zahl ein Bit für das Vorzeichen „opfern“:
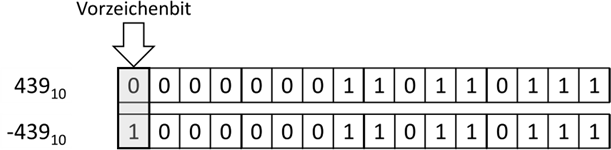
Abb.: 1: "Navier" Ansatz für Vorzeichen im Binärformat
Dieser Ansatz hätte nun zwei entscheidende Nachteile. Erstens gibt es die 0 zweimal, nämlich + und – 0, was unlogisch
scheint – zumindest bei ganzen Zahlen. Weiterhin müssten wir eine unnötig komplizierte Logik einbauen, wenn wir eine
negative und eine positive Zahl addieren möchten. Mit einer einfachen Addition auf Binärebene würde ein Fehler
herauskommen:
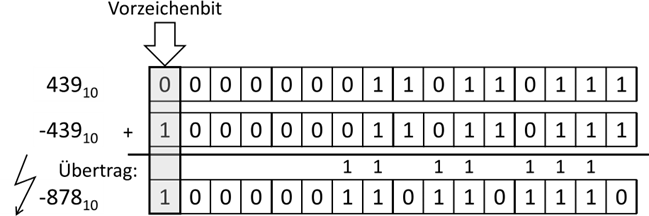
Abb.: 2: Binäre Addition
Wenn wir binär addieren, schreiben wir wie im Dezimalsystem die Zahlen rechtsbündig untereinander und addieren Stelle
für Stelle. Bei der kleinsten Stelle addieren wir 12 +
12, macht 102, weshalb wir die 0 als Ergebnis übernehmen
und den Übertrag 1 notieren (…dies würde Dezimal genauso laufen, wenn wir bspw. die 4 plus 6 rechnen würden. Das
Ergebnis wäre 10 im Dezimalsystem, weshalb wir unter 4+6 die 0 notieren würden und den Übertrag 1 hätten). In der
nächsten Spalte addieren wir 12 + 12 plus den Übertrag
12, macht 112. Dadurch haben wir als Ergebnis 1 und wieder
den Übertrag 1. Und so gehen wir alle Bits durch. Das Ergebnis wäre dann 1000.0011.0110.11102.
Wenn wir das erste Bit als Vorzeichen interpretieren würden, hätten wir somit als Ergebnis -878, was natürlich nicht der
erwarteten 0 entspricht. Insofern ist das Vorzeichenbit für ganze Zahlen erstmal keine gute Idee.
Die Frage ist nun, ob es überhaupt gehen würde, zwei positive Zahlen so zu addieren, dass die 0 herauskommt. Mathematisch ist
dies natürlich unmöglich. Allerdings können wir nun von der Beschränktheit der Bitbreite von Speicherzellen profitieren. Wie
wäre es denn, wenn das Ergebnis nicht 16 Bitstellen lang wäre, sondern 17, beispielsweise
1.0000.0000.0000.00002 (dezimal 65.536). Da wir nur 16 Stellen speichern können, müssten wir
jetzt die linke 1 einfach abschneiden und der Rechner würde jetzt tatsächlich die 0000.0000.0000.00002
ablegen. Das heißt, wir würden die Rechnung 439 + (-439) = 0 umstellen in 439 + (???) = 65.536. Wenn wir nun das ???
ausrechnen, haben wir eine mögliche Darstellung der Zahl -439. Das Bitmuster müsste 65.536 – 439 = 65.097 in Binär sein.
Probieren wir es:
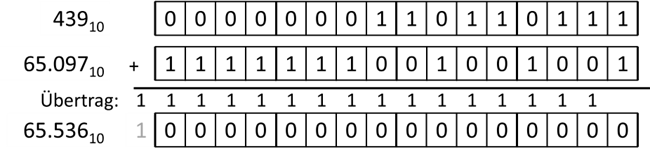
Abb.: 3: Addition von Zweierkomplement
Wenn wir also die Bitkombination 1111.1110.0100.10012 als -439 interpretieren, dann würde
die Addition dieser Bitkombination mit 0000.0001.1011.01112 tatsächlich
1.0000.0000.0000.00002 ergeben, wobei der Übertrag auf die 17. Stelle einfach ignoriert
werden würde. Diese Darstellung einer negativen Zahl bezeichnet man als „Zweierkomplement“ und ist eine übliche
Kodierung von negativen ganzen Zahlen. Die Bildung des Zweierkomplements aus einer Zahl (sprich die Bildung der
negativen Darstellung einer Zahl) ist relativ einfach – man invertiert alle Bits (sprich aus jeder 1 wird die 0 und aus
jeder 0 wird die 1). Anschließend addiert man noch die 1 und ist fertig.
Was bedeutet dies nun für unsere Zahlenmenge? Schreiben wir doch einfach mal die Wertebereiche hin:
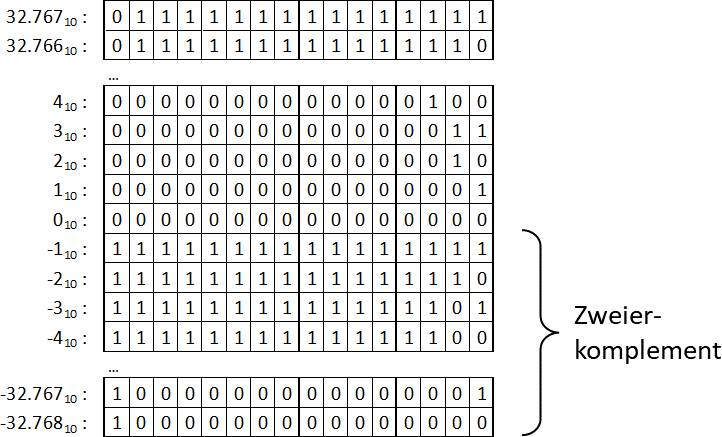
Abb.: 4: Wertebereich bei 16Bit mit Zweierkomplement
Der Wertebereich läuft also von -32.768 bis 32.767, was bedeutet, dass die 216 Kombinationen in eine positive und
eine negative Hälfte gesplittet wird, wobei die 0 der positiven Hälfte zugeordnet wird. Deshalb ist hier der größte
positive Wert die Hälfte von 216 minus 1. Interessant ist auch, dass wir nun doch wieder
ein Bit haben, aus dem wir das negative Vorzeichen extrahieren könnten – wieder das linke Bit. Alle anderen Bits
im Bereich der negativen Zahlen werden aber durch das Zweierkomplement gebildet. Wenn wir also eine negative Zahl,
bspw. die -35 haben, so ist das der Binärwert 1111.1111.1101.11012. Wir erkennen, dass
das erste Bit 1 ist. Also ziehen wir 1 ab, was 1111.1111.1101.11002 ergibt und drehen
jedes Bit um. Somit erhalten wir was 0000.0000.0010.00112, den Binärwert für 35.
Die Frage ist nun, was bringt mir als Programmierer dieses Wissen? Hier gibt es zwei Bereiche, in denen dieses
Wissen wichtig ist. Der erste Bereich ist, wenn wir in unseren Programmen ganze Zahlen verarbeiten wollen und mit
einer Programmiersprache arbeiten, bei denen wir die „Datentypen“ angeben müssen. Hier ist es wichtig zu wissen,
welchen Datentyp wir nehmen können, welchen Speicherplatz der ausgewählte Datentyp verwendet und welcher Wertebereich
daraus resultiert. Gehen wir mal davon aus, dass wir Zahlen von –1 Milliarde bis +1 Milliarde in einer Variablen
erwarten. Hierfür ist der Datentyp „Integer“ (oder oft kurz „int“ genannt) geeignet. Dieser Datentyp hat eine Bitbreite
von 32 Bit, wodurch wir 232 = 4.294.967.296 Bitkombinationen abbilden können. Daraus ergibt sich ein Wertebereich von:
- (232 / 2) = -2.147.483.648 bis + (232 / 2) - 1 = +2.147.483.647
Wir werden später noch alle gängigen Datentypen beleuchten. Der zweite wichtige Punkt zu verstehen ist, wie der Computer mit Zahlenüberläufen
umgeht. Sehen wir uns hierfür mal folgendes in C geschriebene Programm an:
Listing 1: Überlauf int in C
Kurze Erklärung der Codezeilen: In der ersten Zeile erstellen wir eine Variable vom Datentyp int, wodurch sie
den von uns festgestellten Wertebereich hat. Weiterhin schreiben wir den größtmöglichen Wert in die Variable, nämlich
„2147483647“. In der nächsten Zeile erhöhen wir den Wert in dieser Variablen um 1. Binär wird folgendes
gerechnet:
0111.1111.1111.1111.1111.1111.1111.11112 + 1 = 1000.0000.0000.0000.0000.0000.0000.00002“. Das ist aber eigentlich eine negative Zahl, und zwar die -2.147.483.648. In der letzten Zeile geben wir die Zahl einfach auf der Konsole aus, wobei die Interpretation als Zahl mit Vorzeichen durchgeführt wird (%d).
0111.1111.1111.1111.1111.1111.1111.11112 + 1 = 1000.0000.0000.0000.0000.0000.0000.00002“. Das ist aber eigentlich eine negative Zahl, und zwar die -2.147.483.648. In der letzten Zeile geben wir die Zahl einfach auf der Konsole aus, wobei die Interpretation als Zahl mit Vorzeichen durchgeführt wird (%d).
Wenn wir das Programm starten, sehen wir auf der Konsole folgende Ausgabe:
Wir können also exakt nachvollziehen, warum unsere Variablen ein derartiges, auf den ersten Blick „merkwürdiges“ Verhalten zeigen. Es gibt
zwar vereinzelt Systeme, welche bei einem solchen „Überlauf“ einen Fehler generieren. Bei sehr vielen Programmiersprachen können wir aber
genau das oben gezeigte Verhalten beobachten. Die Zahlen liegen also in einer Art Kreis. Dies lässt sich sehr schön bei einem fiktiven
Datentyp veranschaulichen, der nur 4 Bits zur Verfügung hätte:
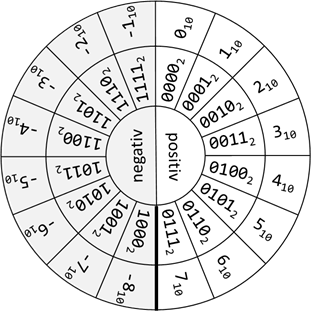
Abb.: 5: Positive und negative Binärzahlen im Zahlenkreis
Einen Nachteil haben wir aber bei dieser Darstellung von negativen Zahlen. Der Prozessor muss beim größer/kleiner Vergleich das vorderste
Bit separat auswerten, da vom Bitmuster her die negativen Zahlen größer sind als die positiven. Die Designer der Computersysteme hatten
also die Wahl, die negativen Zahlen oder den Vergleich zu optimieren – im Fall der ganzen Zahlen haben sie sich für die Optimierung der
negativen Zahlen entschieden.

Ganzzahlige Typen
Sehen wir uns kurz die gebräuchlichsten Datentypen für ganzzahlige Werte und den zugehörigen Wertebereiche an. Bei den Wertebereichen
unterscheiden wir, ob der Datentyp auch negative Werten akzeptieren soll (also mit negativen Vorzeichen, genannt „signed datatype“) oder nur
die positiven Werte (also ohne negative Vorzeichen, genannt „unsigned datatype(1)“). Unsigned Datentypen werden – sofern sie unterstützt
werden – wie in C durch das Voranstellen von „unsigned“ (also bspw. unsigned int) erstellt oder wie in C# nur durch
ein „u“ vor dem Datentyp (also bspw. uint). In manchen Fällen schreibt man bei „signed“ noch ein s davor, wie
bspw. in C# bei einem signed byte „sbyte“. Dies liegt daran, dass Bytes im regelfall als unsigned Werte
interpretiert werden.
| Name: | Anzahl Bits: | Minwert (signed): | Maxwert (signed): | Minwert (unsigned): | Maxwert (unsigned): |
|---|---|---|---|---|---|
| byte | 8 | -128 | 127 | 0 | 255 |
| short | 16 | -32.768 | 32.767 | 0 | 65.536 |
| int | 32 | -2.147.483.648 | 2.147.483.647 | 0 | 4.294.967.296 |
| long | 64 | -9.223.372.036.854.775.808 | 9.223.372.036.854.775.807 | 0 | 18.446.744.073.709.551.616 |
Tabelle 1: Die wichtigsten ganzzahligen Datentypen(2)
(2) Die Wertebereiche beziehen sich auf Java, C# und C auf einem 32 Bit System
Die Namen dieser Datentypen sind bei vielen gängigen Programmiersprachen gleich oder zumindest ähnlich.
In Datenbanken findet man aber mitunter die Bezeichnungen „tinyint“ für
„byte“, „shorting“ und
„longint“ (und bei manchen Systemen auch
„mediumint“ für Datentypen, die 24 Bit belegen). Im Zweifelsfall einfach
das Internet befragen.
Nun müssen wir noch über den Umgang mit diesen Datentypen innerhalb des Codes sprechen. Grundsätzlich gilt
ja, dass die Bitrepräsentation auf dem Speicher durch den Computer erstmal interpretiert werden muss.
Wenn wir beispielsweise eine Variable auf dem Bildschirm ausgeben wollen, so können wir es wie in unserem
obigen C Programm über
printf("Wert: %d", zahlVariable); durchführen. Das
„%d“ führt zur Interpretation der Zahl als
„signed digit“. Wenn wir die Ausgabe anstatt mit
„%d“ mit „%u“ durchführen, wird das Bitmuster als
„unsigned digit“ ausgegeben. Prüfen wir dies einmal nach:
Listing 2: Signed und unsigned Interpretation von int
Kurze Erklärung der Codezeilen: In der ersten Zeile erstellen wir eine Variable vom Datentyp
int, was in C automatisch eine
„signed int“ Variable ist. Wir belegen sie mit der -1, was das Bitmuster:
1111.1111.1111.1111.1111.1111.1111.11112 ergibt. Danach geben wir die Zahl über
%d aus, somit als signed. Nun geben wir einen Zeilenumbruch mit
\n (new line) aus. Am Schluss wird nochmal eine Ausgabe durchgeführt, diesmal mit
%u, als unsigned.
Wenn wir das Programm starten, sehen wir auf der Konsole folgende Ausgabe:
Der zweite Wert entspricht also genau dem Bitmuster für 32 mal die 1, wenn wir es nicht als Zweierkomplement
interpretieren. Man muss dem Computer in diesem Fall also explizit mitteilen, wie er die Zahl zu interpretieren
hat. In Programmiersprachen wie Java hat man letztendlich komplett auf die Umsetzung von unsigned Datentypen
verzichtet, wodurch man diesen Problemen von vorneherein aus dem Weg geht. Ob das nun eine Erleichterung oder
eher ein Hindernis ist, muss jeder für sich selbst entscheiden.
Der letzte zu verstehende Punkt ist, wie Zahlen im Code gelesen werden. Wir wissen ja bereits, dass alles,
was in unserem Code geschrieben und kompiliert wird, während der Ausführungszeit im Speicher landet. Bei
Variablen müssen wir den Datentyp, zumindest bei typisierten Sprachen, explizit angeben. Dies erfolgt bei
fast allen Programmiersprachen mit dem Voranstellen des Datentyps vor den Variablennamen. Folgender Code
sorgt also dafür, dass während der Laufzeit ein Platz im Speicher des Rechners exklusiv für die folgende
Variable „reserviert“ wird – man nennt diesen Vorgang „Deklaration“:
Listing 3: Deklaration einer int Variablen
Durch diese Deklaration existiert nun diese Variable – allerdings nur innerhalb des Gültigkeitsbereiches,
welcher bei den meisten Programmiersprachen durch geschweifte Klammern definiert wird. Das Klammernpaar
in dem die Deklaration erfolgt bestimmt durch die schließende Klammer, wo die Gültigkeit aufhört. In
unseren ersten Programmen hatten wir aber erstmal nur ein Klammernpaar, weshalb sich die Fragestellung der
Gültigkeit erstmal nicht stellt. Basierend auf dem Datentyp kann der Computer nun feststellen, wie viel
Speicherplatz diese Variable benötigt – in unserem Fall „32 Bit“. Weiterhin kann der Rechner jetzt auch
den Umgang mit dieser Variablen „planen“. Wenn wir beispielsweise den Inhalt der Variablen mit einer Zahl
im Sinne von „größer“ vergleichen, weiß der Rechner aufgrund der Zweierkomplementdarstellung wie er mit
negativen Werten umzugehen hat. Allerdings kann der Rechner diesen Vergleich erst dann sinnvoll durchführen,
wenn wir in die Variable einen Wert hineinschreiben. Tun wir dies nicht, so würden wir mit einer
sogenannten „uninitialisierten“ Variablen arbeiten. Manche Programmiersprachen, wie beispielsweise C,
erlaubend dies. Allerdings kommen dann unerwartete Ergebnisse heraus. Folgendes Programm wurde auf meinem
Rechner mit einem simplen Compiler kompiliert und zweimal hintereinander gestartet(4):
(4) Der g++ Compiler würde manuell eine Initialisierung mit 0 einfügen, weshalb wir mit diesem Compiler
dieses Phänomen nicht nachstellen können.
Listing 4: Deklaration und Ausgabe einer int Variablen ohne Initialisierung in C
Ausgabe nach erstem Start:
Ausgabe nach zweitem Start:
Dies liegt daran, dass durch den Code, der durch den C Compiler erzeugt wird, der Computer angewiesen wird,
einen Platz auf dem Speicher zu reservieren. Und genau das macht der Rechner. Wenn nun zufällig in der
Speicherzelle der Wert 2514944 steht, dann hat die Variable automatisch auch diesen Wert. Dies zeigt uns
auch gleich, was eine „Variable“ eigentlich ist. Sie ist ein Platzhalter in unserem Code, der später zur
Laufzeit durch die Adresse des Speicherplatzes ersetzt wird. Da wir während des Programmierens nicht wissen
können an welcher Stelle zur Laufzeit der Wert liegen wird, arbeiten wir eben mit diesem Platzhalter.
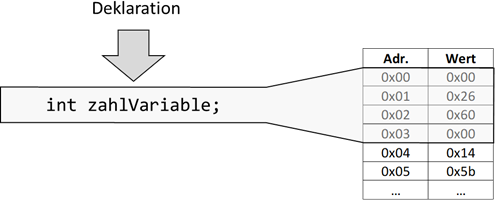
Abb.: 6: Deklaration und Speicherallokation
Wenn wir aber nicht genau sagen, was wir in dieser Speicherzelle haben wollen, so wird einfach das
verwendet, was bei einer vorausgegangenen Nutzung dieses Speicherbereiches noch drinnen steht. Bei einem
erneuten Start dieser Software ist es dann möglich, dass der Computer einen ganz anderen Speicherplatz für
diese Variable aussucht, weshalb dann auch ein anderer Wert zu beobachten ist. Andere Programmiersprachen
würden diesen Code – also Deklaration der Variablen ohne Wertzuweisung und anschließendes Auslesen der
Variablen – bereits beim Kompilieren nicht akzeptieren. Folgender Javacode würde also nicht kompilierbar sein:
Listing 5: Deklaration und Ausgabe einer int Variablen ohne Initialisierung in Java
Erst wenn wir eine initiale Belegung des Wertes vorsehen, wird es funktionieren:
Listing 6: Deklaration, Initialisierung und Ausgabe einer int Variablen in Java
Da diese initiale Belegung so wichtig ist, hat sie auch einen eigenen Begriff bekommen:
„Initialisierung“. Meist macht man die Initialisierung in der gleichen Zeile wie die Deklaration:
Listing 7: Kombination Deklaration und Initialisierung in Java
Jetzt fehlt uns nur noch ein Puzzleteil für das Verständnis beim Umgang mit ganzen Zahlen. Wenn wir davon ausgehen, dass
alles, was in unseren Programmen vorhanden ist im Speicher abgelegt werden muss, dann benötigen wir streng genommen für
den folgenden Code mindestens zwei Speicherzellen:
Listing 8: Kombinierte Rechnung und Ausgabe in Java
Eine wird im Datenspeicherbereich für die Variable benötigt – so viel ist sicher. Es gibt aber noch eine zweite. Im
Programmspeicherbereich muss auch noch der Wert „3“ hinterlegt werden. Und für diesen Wert gilt das gleiche wie für
die Variablen. Sie muss einen Datentyp haben! Nun haben wir aber keinen Datentyp für diese Zahl deklariert. Woher soll
nun der Rechner wissen, welcher Datentyp hier gemeint ist? Die Antwort ist – er kann es nicht wissen. Es wäre zwar
möglich, aus dem Kontext dies zu „erraten“ aber die Lösung dieses Problems ist viel profaner. Die meisten
Programmiersprachen gehen einfach von einem Standardfall aus. Bei ganzzahligen Datentypen ist dies meist
int. Wenn wir die obere Codezeile also ansehen, dann wird die 3 intern einfach als
int Wert angenommen und als Konstantwert abgelegt. Wir werden später noch über das Thema „Typecast“ sprechen, worunter
wir die Umwandlung der Werte von dem einen Datentypen in einen anderen verstehen. Dieses Phänomen ist streng genommen
auch für die Nutzung von Konstantwerten bei der Initialisierung wichtig. Für jetzt genügt erstmal die Vorstellung, dass
jede konstant angegebene Zahl ohne Nachkommastellen im Code als
int interpretiert wird(5)
(5) Diese Angaben gelten für die meisten Programmiersprachen.
Wenn dem aber so ist, dann müssten wir spätestens mit diesem Code in Java ein Problem bekommen:
Listing 9: Fehlerhafte long Zuweisung in Java
Und in der Tat gibt dieser Code in Java einen Compilerfehler. Der Hintergrund ist, dass die konstanten Zahlen im Code
ja als
int interpretiert werden und der maximale Wert von
int ist nun mal 2.147.483.647, was eindeutig kleiner ist als 10.000.000.000. Um nun trotzdem eine
long Variable mit einem größeren Wert als 2.147.483.647 konstant belegen zu können, müssen wir hinter der Zahl ein
„l“ für
„long“ anhängen. Dadurch wird die Konstante als
long interpretiert:
Listing 10: Korrekte long Zuweisung in Java

Gleitkommazahlen
Damit haben wir alles Notwendige für ganzzahlige Werte in unseren Programmen verstanden. Was wir nun noch brauchen, ist
eine Darstellung für Zahlen mit einem Komma. Für die Mathematiker unter uns: leider kann der Computer keine reellen
Zahlen aus der Zahlenmenge
ℝ verwenden – wir müssen uns
mit rationalen Zahlen aus der Menge ℚ
begnügen. Das liegt im Wesentlichen wieder an der Beschränktheit unserer Datentypen. Sehen wir uns erstmal den Aufbau
von Kommazahlen im Dezimalsystem an. Wenn wir beispielsweise die Zahl 342,284 nehmen, so können wir diese als Summe der
einzelnen Ziffern multipliziert mit dem Stellenwert darstellen:
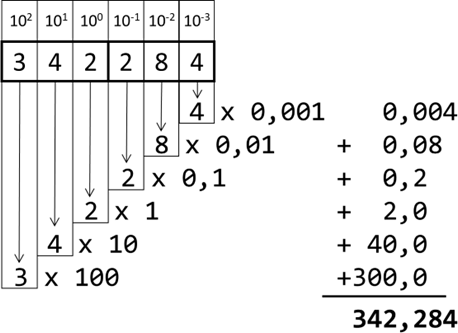
Abb.: 7: Zerlegung einer Dezimalbruchzahl in die Einzelwerte
Machen wir mal ein ähnliches Beispiel im Binärformat. Nehmen wir bspw. die Zahl 1011,1012 und zerlegen sie entsprechend:
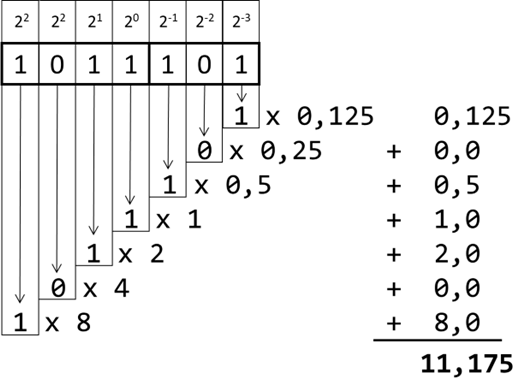
Abb.: 8: Zerlegung einer Binärbruchzahl und Umrechnung in Dezimal
Wie wir sehen, ist der Algorithmus zur Umrechnung der gleiche, wir tauschen wieder lediglich die Basis aus. Wir sind
also nun in der Lage, auch Binärbruchzahlen (also Zahlen mit Komma) in Dezimal umzuwandeln. Das „unschöne“ der oben
gezeigten Darstellung ist, dass wir dem Rechner mitteilen müssten, wie viele Vor- und Nachkommastellen vorzusehen sind.
Hier hilft uns jetzt die wissenschaftliche Zahlendarstellung in Exponentenschreibweise. Die Dezimalbruchzahl 342,284
kann auch wie folgt dargestellt werden:
342,284 = 3,42284 x 102
Diese Schreibweise hat zwei Informationen. Erstmal die Ziffernstellen vor dem „x“, welche man auch als „Mantisse“
bezeichnet. Die Mantisse hat vor dem Komma immer eine einzige Stelle ungleich 0, in unserem Fall 3,42284. Die Zehnerpotenz
gibt lediglich an, um wie viele Stellen das Komma nach rechts (positiver Exponent) oder nach links (negativer Exponent) zu
verschieben ist. In unserem Fall sind es zwei Stellen nach rechts, wodurch die ursprüngliche Zahl 342,284 herauskommt.
Dies sollte somit auch erklären, warum es nicht sinnvoll ist, bei der Mantisse vor dem Komma eine 0 zu platzieren.
Bei 0,342284 x 103 wäre die Angabe zwar richtig, aber nicht normiert, genauso wie
0,000342284 x 106 oder 342284,0 x 10-3. Man würde die Schreibweise
mit Exponent und Mantisse auch als „Fließkommazahl“ oder im Englischen „floating point number“ bezeichnen, weshalb ein
möglicher Datentyp für solche Zahlen auch „float“ heißt(6).
(6) Im Gegensatz zu „Festkommazahlen“, bei denen die Anzahl der Nachkommastellen fixiert ist.
Übertragen wir diesen Gedanken mal in das Binärsystem. Wir geben die Mantisse an, indem wir vor dem Komma eine einzige
Stelle ungleich 0 setzen. Das ist aber im Binärsystem immer die 1, da es neben der 0 ja nur die 1 gibt. Diesen Sachverhalt
nutzt der Computer, indem er die führende 1 gar nicht speichert – er weiß ja, dass es die 1 sein muss – sie wird also
implizit angenommen. Dadurch können wir zwar theoretisch keine „0“ mehr darstellen, aber dafür zeige ich gleich noch eine
Lösung. Nun wird die Position des Kommas angegeben. Unsere Zahl 1011,1012 würde also (1),011101 x 23 lauten. Das bedeutet
somit, wir benötigen mindestens zwei Informationen in unserer Speicherzelle des Computers, die Mantisse und den Exponenten.
Jetzt gibt es aber noch zwei Besonderheiten, welche die Vorzeichen angehen. Beginnen wir mit dem Exponenten. Dieser kann
ja positiv oder negativ sein. Der Ansatz, negative Exponenten mit dem Zweierkomplement abzubilden geht man hier nicht,
sondern man nimmt die Binärzahl und zieht einfach einen festen Wert ab, bei einfachen Fließkommazahlen ist dies der Wert
127. Wenn wir bspw. im Speicherbereich des Exponenten den Wert 130 binär abgelegt haben, dann ist der Exponent
130 – 127 = 3 – also 23. Dies hat den Vorteil, dass die Vergleichbarkeit bezüglich Größe von Zahlen einfacher ist. Dies
ist also eine andere Priorisierung als bei den ganzen Zahlen, wo der simplere Umgang mit negativen Zahlen wichtiger war.
Die -3 würde bspw. mit der 124 abgelegt werden und der Vergleich -3 < 3 würde im Rechner mit 124 < 130 durchgeführt werden.
Ein weiterer Punkt ist das Vorzeichen der Mantisse. Auch diese ist nicht im Zweierkomplement abgelegt. Man hat sich hier
für ein Vorzeichenbit entschieden, weshalb es tatsächlich die +0 und die -0 gibt – hier wieder für die Mathematiker
interessant, welche durchaus die positive oder negative 0 kennen
(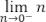 ). In Java kann man nun
in der Tat die -0.0 provozieren:
). In Java kann man nun
in der Tat die -0.0 provozieren:
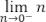 ). In Java kann man nun
in der Tat die -0.0 provozieren:
). In Java kann man nun
in der Tat die -0.0 provozieren:
Listing 11: Negative 0 bei Floatvariablen in Java
Wenn dieser Code ausgeführt wird, sehen wir auf der Konsole tatsächlich -0.0. Das hat zwar wenig Relevanz für die
Praxis, beweist aber den inneren Aufbau von
float Datentypen. Würden wir die
zahlVariable als
„int“ deklarieren, würde die Ausgabe nur 0 sein. Sehen wir uns der Vollständigkeit halber den Aufbau einer 32 Bit
Gleitkommazahl nun mal an:

Abb.: 9: Aufbau 32 Bit Float Zahl
Es gibt nun noch ein paar Sonderfälle, welche als festes Bitmuster definiert wurden:
| Zahl: | Vorz.: | Exponent: | Mantisse: | Erklärung: |
|---|---|---|---|---|
| 0.0 | 0 | 0 | 0 | Positive 0 (Achtung – die implizite 1 wird ignoriert!) |
| -0.0 | 1 | 0 | 0 | Negative 0 (Achtung – die implizite 1 wird ignoriert!) |
| NaN | 0 oder 1 | 255 | ungleich 0 | Keine gültige Zahl (Not a Number) |
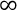 |
0 | 255 | 0 | Plus Unendlich |
-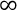 |
1 | 255 | 0 | Minus Unendlich |
Tabelle 2: Sonderwerte bei float Zahlen
Interessant ist hier, dass wir sowohl unendlich als auch
„NaN“ (spricht „Not a Number“) abbilden können. Vor allem die Option von +/- Unendlich bietet jetzt die
Möglichkeit, die Rechnung 1.0/0.0 auszugeben. Mathematisch ist es eigentlich nicht definiert, aber bspw. die
Java Macher lassen hier bei der Ausgabe auf der Konsole „Infinity“ erscheinen. Ob dies nun sinnvoll ist oder
nicht – sprich ob man diese Funktionalität nutzt – muss wieder mal jeder für sich entscheiden. Gehen wir nun
mal auf die eigentlichen Besonderheiten von Gleitkommazahlen ein, die uns beim Programmieren durchaus Kopfzerbrechen
bereiten können. Dazu müssen wir vorab darüber sprechen, wie der Computer aus einer Dezimalzahl eine Binärzahl erstellt.
Da wir mit Gleitkommazahlen arbeiten, würde die Erklärung des Algorithmus für die Nachkommastellen genügen, der
Vollständigkeit halber möchte ich aber über die ganzen Zahlen und über die Nachkommastellen sprechen.
Eine Grundüberlegung in der Mathematik ist, dass wir zwar mit Zahlen arbeiten und dort beliebige Rechenverfahren
anwenden können – die Darstellungsart der Zahlen hierbei jedoch irrelevant ist. Frei nach dem Motto
5 + 4 = 9 ist genauso richtig wie V + IV = IX oder 1012 + 1002 = 10012.
Insofern können wir die Algorithmen erstmal in unserem vertrauten Zahlensystem, dem Dezimalsystem ansehen, bevor wir sie in
das Binärsystem übertragen. Ich möchte also wissen, welche Dezimalziffern in einer Zahl stecken – sagen wir die 342.
Natürlich sehen wir die Ziffern durch einen einzigen Blick, schließlich liegt die Zahl ja im Dezimalsystem vor.
Trotzdem überlegen wir uns einen Algorithmus, der uns Ziffer für Ziffer liefert. Hierzu benötigen wir einen speziellen
Rechenoperator, genannt „Restoperation“. Für diejenigen, die diesen Operator nicht kennen – keine Angst – ihr kennt ihn
sehr wohl, nur unter einem längeren Namen, eben der „Rest der ganzzahligen Division“, so wie es in der Grundschule gelehrt
wird. Dort haben wir gesehen, dass beispielsweise 23 : 7 = 3, Rest 2 ist. Rest 2 deshalb, weil die 7 dreimal in 23 reinpasst,
was 3x7 = 21 ergibt. 23 – 21 wiederum ergibt 2, genannt „Rest“ oder englisch „Remainder“. Deshalb kann man schreiben,
23 Rem 7 = 2. In vielen Programmiersprachen ist das Symbol hierfür das Prozentzeichen
„%“, weshalb in Computerprogrammen geschrieben wird:
23%7=2. Dieser „Restoperator“ wir gerne auch als „Modulo“ Bezeichnet, was allerdings nur für positive Zahlen gilt. Da es aber
von den Begriffen her klarer (und vor allem gebräuchlicher) ist, verwende ich ab hier den Begriff „Modulo“ und werde bei den Operatoren noch Näheres klären.
Nun können wir also einen kleinen Algorithmus definieren, der uns die einzelnen Zahlen auswirft:
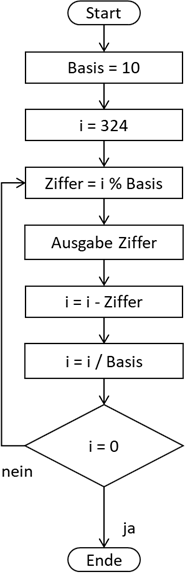
Abb.: 10: Extraktion einzelner Dezimalstellen
Gehen wir das Ganze mal durch. Wir sind im Zehnersystem und haben somit die Basis = 10. Dann legen wir eine Zahl in
„i“ fest.
„i“ steht im Regelfall für eine int Zahl – sprich eine Zahl vom Datentyp Integer und somit eine Zahl ohne
Nachkommastellen. Dann spielen wir den Algorithmus mal durch.
- Setzen der Basis auf 10
- Ablegen der Zahl 324 in Variable i
- i = 324 modulo 10 ergibt: 4 (aha – dies ist also unsere erste extrahierte Ziffer)
- Ausgabe ist: 4
- i = 324 – 4 ergibt 320 (wir haben also „nur“ den Ziffernwert entfernt)
- i = 320 / 10 ergibt 32 (somit wurde das „Komma“ um eine Stelle nach links verschoben)
- i ist nicht 0, weshalb der Algorithmus wiederholt wird
- i = 32 modulo 10 ergibt: 2 (plus Ausgabe 2, die zweite extrahierte Ziffer)
- i = 32 – 2 = 30
- i = 30 / 10 = 3
- i ist nicht 0, weshalb der Algorithmus wiederholt wird
- i = 3 modulo 10 ergibt: 3 (plus Ausgabe 3, der dritten extrahierten Ziffer)
- i = i – 3 = 0
- i = 0 / 10 = 0
- i ist 0, weshalb der Algorithmus endet
Nun haben wir auf eine zugegebenermaßen recht komplizierte Art die drei Ziffern unserer Zahl 324 extrahiert.
Der Vorteil unseres Algorithmus ist aber, dass wir jetzt lediglich die Basis austauschen müssen, um die Umrechnung in
einem anderen Zahlensystem zu realisieren. Im Binärsystem wäre die Basis nun 2. Ich spare mir an dieser Stelle die
nochmalige Abbildung des Algorithmus mit der ausgetauschten 2 als Basis. Dafür zeige ich das Java Programm, welches
diesen Algorithmus umsetzt:
Listing 12: Algorithmus für ganzzahlige Binärumwandlung in Java umgesetzt
Kurze Erklärung der Codezeilen: Die Deklaration und Initialisierung von ganzzahligen Datentypen dürfte inzwischen klar
sein. Das
do zusammen mit dem
while ist eine fußgesteuerte Wiederholungsschleife. Sie gehört zu den „Kontrollstrukturen“, welche wir später genauer
behandeln werden. Was hier passiert ist, dass der Code innerhalb der geschweiften Klammern (des „Schleifenrumpfes“) so
lange ausgeführt wird, solange die Bedingung nach dem
while erfüllt ist, nämlich
i!=0 (das bedeutet „i ungleich 0“). Innerhalb des Schleifenrumpfes wird eine Variable für die auszugebende Ziffer
deklariert und über modulo berechnet, dann mit
„print“ ausgegeben, was in Java eine Ausgabe ohne Zeilenumbruch ist. Anschließend wird
i entsprechend des Algorithmus angepasst.
Die Ausgabe auf der Konsole ist entsprechend:
Der Wert ist nun rückwärts zu lesen, also 1010001002, was bei Umrechnung wieder die 324
ergibt. Soweit ein relativ einfacher und effektiver Algorithmus für die Umrechnung in andere Zahlensysteme. Nun fehlen
uns noch die Nachkommastellen. Gehen wir diesmal wieder von einer Dezimalzahl aus, der 0,875. Wir wollen nun wieder
einen Algorithmus untersuchen, der uns die einzelnen Ziffern liefert:
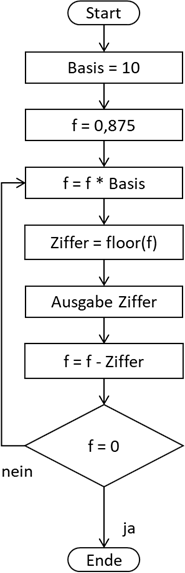
Abb.: 11: Algorithmus zur Extraktion von Nachkommastellen
Gehen wir auch hier den Algorithmus Schritt für Schritt durch:
- Setzen der Basis auf 10
- Ablegen der Gleitkommazahl 0,875 in f
- f wird gesetzt als 0,875 x 10 = 8,75
- Abschneiden der Nachkommastellen („floor“) der Zahl f = 8 (das ist nun die extrahierte Ziffer)
- Ausgabe der Ziffer 8
- f wird gesetzt als 8,75 – 8 = 0,75
- f ungleich 0 weshalb die Schleife wiederholt wird
- f wird gesetzt als 0,75 * 10 = 7,5
- Ziffer wird durch Abschneiden auf 7 gesetzt und ausgegeben
- f wird gesetzt auf 7,5 – 7 = 0,5
- f ist ungleich 0, also Wiederholung
- f wird gesetzt als 0,5 * 10 = 5,0
- Ziffer wird durch Abschneiden (auch wenn es nicht notwendig ist) auf 5 gesetzt und ausgegeben
- f wird gesetzt auf 5,0 – 5 = 0
- f ist 0, das Programm endet
Listing 13: Algorithmus für ganzzahlige Binärumwandlung
Kurze Erklärung der Codezeilen: Im Prinzip funktioniert der Code wie im Listing 12. Das
„f“ nach der 0.875 ist die Indikation, dass wir eine float Konstante nutzen. Das ansonsten einzig zu erwähnende ist die
Zeile
int ziffer = (int)f;. Hier wird der Variableninhalt der float Variablen
„f“ in eine int Variable
ziffer gezwungen. Da
int keine Nachkommastellen abbilden kann, wird der Nachkommaanteil einfach abgeschnitten.
Wenn wir den Code nun laufen lassen, erhalten wir:
Eigentlich ist es ja 0,1112 Wenn wir nun die Werte 1x2-1 = 0,5, 1x2-2 = 0,25 und
1x2-3 = 0,125 zusammenaddieren, erhalten wir wieder 0,5 + 0,25 + 0,125 = 0,875. So weit, so gut! Jetzt ändern wir aber
unsere Gleitkommazahl „f“ auf 0,4 und sehen was passiert:
Das ist erst einmal eine „Überraschung“. Doch was steckt hier dahinter? Gehen wir die Rechnung mal Schritt für Schritt
durch:
- 0,4 x 2 = 0,8. Abgerundet gibt das die Ziffer 0
- 0,8 – 0 = 0,8
- 0,8 x 2 = 1,6. Abgerundet gibt das die Ziffer 1
- 1,6 – 1 = 0,6
- 0,6 x 2 = 1,2. Abgerundet gibt das die Ziffer 1
- 1,2 – 1 = 0,2
- 0,2 x 2 = 0,4. Abgerundet gibt das die Ziffer 0
Und jetzt kommt das Problem! Wir fangen nun wieder von vorne an! Rein theoretisch würden wir unendlich weiterrechnen (der
Computer hat allerdings abgebrochen, da die interne Zahlendarstellung ja begrenzt ist). Aber was heißt das eigentlich?
Nun die eigentliche Aussage ist, dass im Binärsystem die Zahl 0,4 eigentlich als
0,01102 sprich „null Komma Periode null, eins, eins, null“ ist.
Das heißt, wir würden eigentlich unendlich viele Stellen für die Nachkommastellen benötigen. Dies ist aber aufgrund der
Begrenztheit des Speichers nicht möglich. Intern wird die Zahl (100)100110011001100110011012
dargestellt, was eigentlich 0.4000000059604644775390625 ergibt. Diesen „Fehler“ können wir in der eigentlichen Ausgabe von
0,4 zwar nicht sehen, da sich der Computer um eine korrekte Ausgabe durch interne Rundungsprozesse kümmert, aber wir können
diese „Bemühung“ austricksen, wenn wir einfach folgenden Code ausführen:
Listing 14: Rundungsfehler bei Gleitkommaoperationen
Die Konsolenausgabe ist hier:
Eine Rechnung, die wir ohne Probleme im Kopf korrekt ausrechnen können, führt aufgrund der Ablage im Binärsystem plötzlich
zu einem sehr merkwürdigen Rundungsfehler! Dies bedeutet, dass wir bei der Nutzung von Gleitkommazahlen in unseren
Programmen dem Ergebnis nur bis zu einem gewissen Genauigkeitsgrad trauen können. Das ist zwar erstmal erschütternd,
wirkt sich aber nur bedingt aus, da der prozentuale Fehleranteil sehr gering ist. Sehen wir uns nun mal die beiden
typischen Gleitkomma-Datentypen und den ungefähren Wertebereichen an, wie sie auf den meisten Rechnersystemen zu erwarten
sind:
| Name: | Anzahl Bits: | Anzahl Bits (Exp.): | Anzahl Bits (Mant.)(7): | Wertebereich Exponent: | Wertebereich Mantisse: | Anzahl Stellen Mantisse: |
|---|---|---|---|---|---|---|
| float | 32 | 8 | 23+1 | 10+/-38 | +/- 3,4 | 7 |
| double | 64 | 11 | 52+1 | 10+/-308 | +/- 1,7 | 11 |
Tabelle 3: Ungefähre Wertebereiche von Gleitkommazahlen Datentypen
(7) Anzahl immer + 1, da das implizite Bit mitgerechnet werden muss.
Wir haben also im Regelfall zwei verschiedene Datentypen für Gleitkommazahlen. Wenn wir uns an die ganzzahligen Datentypen
erinnern, war
„int“ der Standardfall für Konstantwerte im Code, wodurch der Wertebereich für fest im Code hinterlegte Zahlen auf
-2.147.483.648 bis 2.147.483.647 festgelegt wurde. Bei größeren Zahlen mussten wir auf
„long“ umsteigen und hier erwarten die Programmiersprachen oft eine Ergänzung. In Java war dies das angehängte
„l“ (siehe Listing 10). Bei den Gleitkommazahlen ist der Standardfall
„double“. Wenn wir also eine Gleitkommazahl im Code hinterlegen, bspw. „0.4“, wird dies im Regelfall als double interpretiert.
Dies hat zur Folge, dass float Zahlen auch mit einem Buchstaben markiert werden müssen – sinnigerweise mit
f:
Listing 15: Korrekte float Zuweisung in Java
Es dürfte bei dem relativ „komplizierten“ Aufbau von Gleitkommazahlen nun klar sein, warum die Prozessorhersteller für
Gleitkommazahlen eigene Hardwarekomponenten im Kern der CPU vorsehen. Wichtig ist jedoch für uns Programmierer, dass
die Rechnungen fehlerbehaftet sind und eine vergleichsweise hohe CPU-Last hervorrufen.
Jetzt bleibt noch die Frage, inwieweit wir eine Rechnung 0,4 * 0,1 ohne einen Rundungsfehler realisieren können. Eine
bereits angedachte Möglichkeit ist, dass wir einfach eine
double Variable nutzen und bei der Multiplikation von zwei Zahlen mit n Nachkommastellen auf n+n Nachkommastellen runden.
Bei 0.4 (also eine Nachkommastelle) * 0.1 (auch eine Nachkommastelle) runden wir auf 1+1 = 2 Nachkommastellen. Hier wäre
ein beispielhafter Code in Java:
Listing 16: Rundungsfehler in Java vermeiden
Wenn wir hier die Konsolenausgabe ansehen, haben wir den korrekten Wert 0.4.
Kurze Erklärung der Codezeilen:
Math.round() rundet den Inhalt der Klammer auf die erste Stelle vor dem Komma, also hat das Ergebnis von
Math.round() keine Nachkommastellen mehr. Wenn wir nun zwei Stellen nach dem Komma runden wollen, müssen wir zuerst das
Komma um zwei Stellen mit
* 100 verschieben. So wird bspw. die 0,4000001 auf 40,00001 welche dann zu 40.0 gerundet wird. In der nächsten Zeile
dividieren wir durch 100, wodurch wir das Komma wieder um zwei Stellen zurückschieben. Die gerundete 40,0 wird dadurch
wieder zur 0,04. Dadurch haben wir auf zwei Stellen nach dem Komma gerundet.

Sonstige Zahlentypen
Eine weitere Möglichkeit sind spezielle Datentypen. In Java gibt es beispielsweise den Typen
„BigDecimal“, mit dem wir korrekt rechnen können, da es sich hier um sogenannte „Festkommazahlen“ handelt. Das Problem
dabei ist, dass wir der
BigDecimal Variablen nicht einfach einen
double oder
float Wert übergeben können, da dieser ja bereits systembedingt die Ungenauigkeit mitbringt. Insofern müssen wir die
Zahlen mit Vor- und Nachkommastellen konstruieren:
Listing 17: Festkommazahlen in Java
Ich habe hier übrigens auf den Konstruktor
BigDecimal("0.4") verzichtet, um das eigentliche Problem hinzuweisen… Die Ausgabe ergibt auch den korrekten Wert 0.4.
Kurze Erklärung der Codezeilen: Bei
BigDecimal handelt es sich um keinen einfachen Datentypen mehr, sondern um eine Klasse. Klassen und Objekte werden wir
später bei der Objektorientierung näher behandeln. Entscheidend beim Code ist, dass wir die 0,4 nicht direkt an den
Konstruktor für die Erzeugung des Objektes übergeben, sondern die 4 (bzw. bei
myDecB die 1). Danach erzeugen wir den Divisor als 10. Durch die Division erhalten wir in den beiden Variablen
myDecA und
myDecB jeweils die korrekten Zahlen 0,4 und 0,1 (jeweils ohne Rundungsfehler). Wenn wir nun diese beiden Zahlen
multiplizieren, erhalten wir den korrekten Wert 0,4 auf der Konsole.
Andere Programmiersprachen gehen hier zum Teil andere Wege. C# nutzt beispielsweise einen
„decimal“ Datentyp, welcher im Wesentlichen eine 1:1 Abbildung eines Gleitkommazahlentyps im Dezimalsystem darstellt.
Um nun diesen Wert überhaupt im Code hinterlegen zu können, muss hier eine neue Kennzeichnung der Zahl mit
„m“ erfolgen. Folgender C# Code würde auch wieder die Ausgabe 0.4 erzeugen:
Listing 18: Nutzung des decimal Datentyps in C#
decimal verhindert zwar nicht alle Rundungsprobleme, liefert aber eine sehr viel höhere
Anzahl von signifikanten Stellen(8) als
double.
(8) 28-29 signifikante Stellen (siehe https://docs.microsoft.com/)

Einzelne Zeichen
Als nächstes kümmern wir uns um Textdaten, die wir im Speicher ablegen wollen. Hier müssen wir vorab aber die kleinste
Einheit von Texten, die einzelnen Zeichen (engl. „character“) ansehen. Beginnen wir mit der offensichtlichen Frage, wie
wir im Speicher Zeichen ablegen wollen, wenn wir doch nur Zahlen in Binärform ablegen können. Die Antwort ist zwar auf
den ersten Blick denkbar einfach, führt aber zu einer Liste an Problemen. Diese „Problemliste“ werden wir endgültig bei
der Behandlung von Filezugriffen angehen, aber die Ursache dieser Herausforderung können wir hier bereits sehen.
Beginnen wir mit einer offensichtlichen Lösung unseres Zahlen- vs. Zeichen Problems. Wenn ein Computer auf dem Bildschirm
einen Text oder Zahlen ausgibt, dann sind das erstmal „nur“ Grafiken – sprich Pixel mit unterschiedlichen Farbwerten.
Folgendes Bild zeigt uns die Zahl 3, wie sie von einem Textverarbeitungsprogramm angezeigt wird, allerdings stark
vergrößert:
Abb.: 12: Screenshot Grafik von Zahl "3"
Wie wir sehen, sind es einfach nur Quadrate unterschiedlicher Farbe. Für den Computer gibt es diese Zahl „3“ nicht,
sie existiert für ihn nur als Bitmuster. Dies bedeutet, dass im Computer irgendwo eine Grafikinformation gespeichert
sein muss, um die Zahl 3 so auszugeben, dass wir sie sehen und interpretieren können. Und das gilt für alle Zeichen,
die wir zu einem Text zusammenfassen können. Nun muss diese Liste an Grafiken irgendwie sinnvoll geordnet werden,
so dass wir kontrolliert und nachvollziehbar darauf zugreifen können. Man hat nun in einer simplen Tabelle festgelegt,
welche Zeichen für unsere Texte existieren sollen und diese wurden durchnummeriert. Dadurch haben wir die Zeichen für
unseren Speicher zugänglich gemacht. Wir speichern also nicht das eigentliche Zeichen (bzw. die Grafik, welche das
Zeichen darstellt), sondern einfach eine Zahl, welche in dieser Zeichentabelle die zugehörige Grafik identifiziert.
Streng genommen gibt es hier noch eine weitere Abstraktionsebene. Es wird eigentlich nicht die Grafik referenziert,
sondern das Zeichen, für das es Grafiken gibt. Somit können wir unsere Zeichen in verschiedenen Schriftarten ausgeben:
Abb.: 13: Unterschiedliche Schriftarten
Wir haben also zwei „Abstraktionsebenen“, die „Zeichentabelle“ (oder auch „codpage“ genannt) in der wir pro Zeichen die
Zahl (oder „ID“) jedes Zeichens ablegen und eine Liste an möglichen Darstellungsarten der Zeichen, die „Schriftarten“:
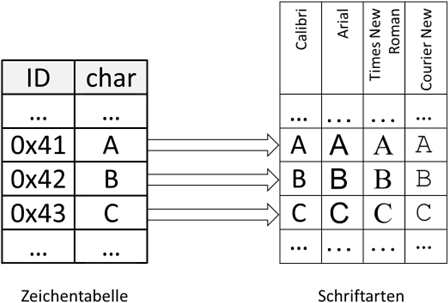
Abb.: 14: Zuordnung Zahl, Zeichen und Schriftart
Die Konsequenz ist, dass wenn eine Schriftart ein bestimmtes Zeichen nicht „kennt“ – sprich keine Grafik dafür gespeichert
hat, dieses Zeichen auch nicht dargestellt werden kann. Für die Standardzeichen werden unsere Rechner bestens gerüstet
sein, wenn es aber um „exotischere“ Zeichen geht, können manche Schriftarten durchaus dazu übergehen lediglich ein „?“
oder ein nichtssagendes Rechteck zu zeigen. Auf die einzelnen Schriftarten wollen wir erstmal nicht näher eingehen –
wir kümmern uns momentan nur um das Wesentliche. Die IDs, welche wir für die einzelnen Zeichen vorsehen, können streng
genommen willkürlich definiert werden. Trotzdem ist eine gewisse Struktur sinnvoll – beispielsweise wollen wir eine
Sortierbarkeit erreichen, weshalb wir die einzelnen Buchstaben sortiert zuordnen. So ist der Buchstabe „A“ die Zahl
4116 (bzw. in Dezimal 65), „B“ kommt danach, also 4216
und so weiter. Die Kleinen Buchstaben fangen bei 6116 an - man muss also einfach
2016 zum Großbuchstaben hinzuaddieren. Die Ids 0 bis 127 (also die ersten
128 Zeichen) sind in der ASCII Zeichentabelle (American Standard Code for Information Interchange) genormt, welche unter
Kapitel XY zu finden ist.
Wir müssen jetzt nur noch festlegen, wie viel Speicherplatz für so eine Zahl der Zeichentabelle vorgesehen sein soll. Damit
legen wir auch fest, wie viele Zeichen wir überhaupt unterscheiden können. Im einfachsten Fall sind es 8 Bit pro Zeichen.
Dies führt dann zu 28 = 256 verschiedenen Zeichen. Dies mag auf den ersten Blick als ausreichend
erscheinen, bei näherer Betrachtung ist es aber eher knapp bemessen. Denken wir bpsw. an die Umlaute, an Zeichen wie
½, ® usw. Ganz zu schweigen von Zeichen für andere Sprachen. Insofern wird es mehrere Tabellen für unterschiedliche Sprachen
bzw. Anwendungsfälle geben müssen, wenn wir auf 8 Bit Datenbreite für Zeichen bestehen. Die ersten 128 Zeichen sind jedoch
immer entsprechend der ASCII Tabelle einheitlich(9). Dies ist insofern sinnvoll, als dass
man hier einen über alle Zeichensätze gemeinsamen Nenner hat. Computercode sollte immer aus dem Zeichenvorrat der ersten 128
Zeichen – sprich dem ASCII Bereich – erstellt werden. Kein ernstzunehmender Programmierer würde auf die Idee kommen, eine
Variable „Zähler“ zu nennen, da der Umlaut „ä“ außerhalb des ASCII Bereiches liegt(10).
Sobald man den Code auf einem anderen System öffnet auf dem eventuell ein anderer Zeichensatz genutzt wird, würde das
„ä“ durch irgendein anderes Sonderzeichen ersetzt werden.
(9) Mit Ausnahme der 12 für die Umdefinition freigegebenen Zeichenpositionen
(10) Zumal man ohnehin Code im Regelfall in Englisch schreibt
(10) Zumal man ohnehin Code im Regelfall in Englisch schreibt
Nun sind diese bei 8 Bit möglichen 256 Zeichen für viele anderweitige Anwendungen zu wenig. Aus diesem Grund hat man
angefangen Datentypen für Zeichen zu definieren, welche den Zeichenvorrat entsprechend erhöhen. Die für die Zukunft am
sichersten funktionierende Definition von Zeichentabellen ist der „Unicode“ Standard, in dem man versucht alle
Zeichen – und das beinhaltet übrigens auch alle asiatischen Schriftzeichen – in einer Norm zu hinterlegen. Die Anzahl der
katalogisierten Zeichen steigt stetig an. Unter https://unicode.org/
findet man nähere Informationen über den aktuellen Stand. Die Computersysteme versuchen nun für ihre interne Verwaltung
genau diese Struktur abzubilden. Hieraus entstanden die „UTF“ Zeichentabellen. Allen voran ist UTF8 (8-Bit UCS
Transformation Format(11)) zu nennen, welches wohl die am häufigsten genutzte Abbildung von
Unicode in Computersystemen ist. UTF8 hat jedoch eine variable Größe – sprich Zeichen aus dem ASCII Bereich benötigen 1 Byte,
alle anderen 2 bis 4 Bytes Speicherplatz. Dies ist für den Datentransport durchaus sinnvoll (und wird hier auch intensiv
eingesetzt). Für das Ablegen von Daten im Rechenspeicher ist es jedoch aufgrund der Größenvarianz der Speicherzellen
umständlich. Die meisten Programmiersprachen nutzen deshalb die UTF16 Codierung, bei der entweder 2 oder 4 Bytes verwendet
werden. Dadurch kann man für die meisten Anwendungsfälle die Zeichen in einem 2 Byte Datentyp speichern, was 216 = 65.536
mögliche Zeichen ergibt. Wenn wir Zeichen aus dem 4 Byte Bereich benötigen, werden meist aufwändigere ergänzende Techniken
benötigt – es werden über ein sogenanntes „surrogate pair“ (dt. „Ersatzpaar“) die zusätzlichen Zeichen adressierbar gemacht.
Da für uns jedoch die 65.536 verschiedenen Zeichen aus dem 2 Byte Datentyp erstmal mehr als
ausreichend(12) sein werden, kümmern wir uns erstmal nicht um die höheren Werte.
(11) UCS: Universal Coded Character Set, wobei das “U” in UTF oft auch als „Unicode“ bezeichnet wird
(12) Die Konsole unserer Windows Version würde ohnehin für die meisten der ersten 32 tausend Unicode Zeichen keine Grafik vorsehen.
(12) Die Konsole unserer Windows Version würde ohnehin für die meisten der ersten 32 tausend Unicode Zeichen keine Grafik vorsehen.
Mit dieser Überlegung haben wir – zumindest für die meisten Programmiersprachen – einen Speicherbedarf für einzelne
Zeichen gefunden, nämlich 2 Bytes oder eben 16 Bit. Dieser Datentyp wird meist mit
„char“ für „Character“ (dt. „Zeichen“) benannt und ist vom inneren Aufbau her nichts anderes als ein Datentyp für
ganze Zahlen – und zwar unsigend, sprich es gibt nur positive Zahlen. Lediglich bei C würde er „nur“ 8 Bit breit sein.
Jetzt müssen wir nur noch klären, wie wir in diese Variablen auch Datenwerte speichern können. Wie unterscheidet der
Computer im Programmcode ein funktionales Zeichen, wie beispielsweise das Istgleich „=“ für die Zuweisung und
ein „=“ Zeichen, welches ich in einer char Variablen ablegen möchte? Diese Unterscheidung ermöglichen die
Anführungsstriche. Sehen wir uns folgenden Code an (der übrigens für die erste Zeile in Java, C, C++ und C#
gleichermaßen aussieht):
Listing 19: Zuweisung eines Konstantwertes in eine char Variable plus Ausgabe in C
Die Ausführung zeigt uns ein „a“ am Bildschirm. Einfache Anführungsstriche werden in fast allen Programmiersprachen als
einzelnes Zeichen für eine
char Variable gewertet. Hier ist aber Vorsicht geboten. Texteditoren, welche nicht für das Erstellen von technischem Code
ausgerichtet sind, versuchen oftmals die einfachen Anführungsstriche durch optisch ansprechendere zu ersetzen, die mitunter
auch außerhalb des ASCII Bereiches liegen. Man schreibt Computer Code also immer mit den dafür vorgesehenen Tools!
Wenn man sich nun die Ausgabeformatierung von
printf ansieht erkennt man, dass
%c hinterlegt werden musste, damit char auch als Zeichen ausgegeben wird. Wenn wir das
%c auf das uns bekannte
„%d“ – also Zahlenausgabe – tauschen, dann gibt uns der Rechner nicht mehr ein „a“, sondern die Zahl 97 – was der ASCII
Code für das Zeichen „a“ ist. Char Variablen sind also wirklich nichts anderes als Zahlenvariablen, nur dass sie nicht
negativ werden können und vom Computer beim Handling als Zeichen interpretiert werden können. Dies heißt aber auch im
Umkehrschluss, dass wir unser „a“ auch direkt über den ASCII Code erzeugen können:
Listing 20: Char Zuweisung über Zahlencode
Dieser Code liefert uns nun ebenfalls auf der Konsole das „a“.
Soweit zu den
char Variablen. Jetzt mag der ein oder andere denken, dass es nicht wirklich sinnvoll ist, einen
Datentyp für nur ein Zeichen zu definieren, schließlich wollen wir ja Texte verarbeiten und das sind viele
zusammenhängende Zeichen. Dieses Rätsel werden wir gleich auflösen, wenn wir über „zusammengesetzte Datentypen“
sprechen. Stand jetzt können wir eben immer nur ein Zeichen speichern.

Logikwerte
Bevor wir uns aber auf die zusammengesetzten Datentypen stürzen, müssen wir noch einen letzten „einfachen“ Datentypen
besprechen, und zwar
„boolean“. Den Namen haben diese Datentypen zu Ehren George Boole erhalten, der durch die formale Beschreibung von binärer
Logik den Grundstein für unsere Computertechnik gelegt hat. Die Variablen vom Typ
„boolean“ oder in manchen Programmiersprachen auch
„bool“ genannt, können nur zwei Werte annehmen, nämlich
„true“ oder
„false“. Intern wird dies meist mit den Zahlenwerten 1 bzw. 0 abgebildet. In C und C++ (und fast allen Skriptsprachen)
liegen hinter
„true“ und
„false“ tatsächlich die Zahlenwerte 0 und 1:
Listing 21: Analyse boolean Variablen in C
Kurze Erklärung der Codezeilen: Da
bool in C ursprünglich nicht vorgesehen war, muss man
stdbool.h inkludieren. In diesem File wird lediglich der
„bool“ Datentyp definiert und
true als 1 bzw.
false als 0 definiert. Bei der Ausgabe sehen wir konsequenterweise auch 1 und 0. Interessant ist aber auch, dass
eine Zuweisung von einer Zahl auf
boolVar möglich ist. Jede Zahl außer 0 wird am Ende als 1 zugewiesen. Wenn wir also
boolVar = -0.1; setzen, erhalten wir die Ausgabe 1.
In C# und Java ist dies wiederum nicht möglich – man hat sich hier um eine klare Trennung der Zahlendatentypen und
bool (oder
boolean) bemüht. In manchen Systemen, wie bspw. einigen Datenbanken, gibt es diesen Datentyp erst gar nicht, man
behilft sich mit einem 8 Bit Ganzzahlentyp und definiert auch hier die „1“ als
„true“ und die „0“ als
„false“. Die
Sinnhaftigkeit dieses Datentyps werden wir erst beim Einsatz in unseren Programmen erkennen. Bis dahin ist die
einzig noch interessante Information über diesen Datentypen, dass er zwar Informationen speichert, welche „nur“ ein
Bit wert sind (also 0 oder 1), aber insgesamt 8 Bit an Speicher belegt. Dies liegt an der Größe der adressierbaren
Einheiten in unserem Computer. Diese ist im Regelfall 8 Bit (also 1 Byte) und demensprechend muss eine boolean Variable
auch mindestens diesen Platz belegen, auch wenn sie weniger Platz benötigen würde.

Überblick primitive Datentypen
Somit haben wir alle relevanten „einfachen“ – man spricht auch von „primitiven“ Datentypen besprochen. Diese Datentypen bilden den Grundstein
jeder Programmiersprache. Alles andere an Datenstrukturen basiert in irgendeiner Weise auf diesen Datentypen. Hier nochmal ein kurzer
Überblick mit den gebräuchlichsten Namen:
| Datentyp: | Bitbreite: | Art der Daten: | Bemerkung: |
|---|---|---|---|
| byte | 8 | Ganzzahlige Werte | Mitunter als „signed“ und „unsigned“ deklarierbar |
| short | 16 | Ganzzahlige Werte | Mitunter als „signed“ und „unsigned“ deklarierbar |
| int | 32 | Ganzzahlige Werte | Mitunter als „signed“ und „unsigned“ deklarierbar |
| long | 64 | Ganzzahlige Werte | Mitunter als „signed“ und „unsigned“ deklarierbar |
| float | 32 | Gleitkommazahlen | Fehlerbehaftet aufgrund Umrechnung aus Basis 2 |
| double | 64 | Gleitkommazahlen | Fehlerbehaftet aufgrund Umrechnung aus Basis 2 |
| char | 32 | Einzelnes Zeichen | UTF16 ohne surrogate(13) |
| boolean | 8 | Logische Zustände | Kann nur „true“ und „false“ annehmen |
Tabelle 4: Wichtige primitive Datentypen
(13) Gilt für die meisten Programmiersprachen
Eine manchmal wichtige Information, gerade für die Zahlendatentypen, waren ja die Minimal- und Maximalwerte, welche bspw. in
int oder
long ablegbar sind. C und C++ liefern uns diese Werte in Konstanten. Den kleinsten ganzzahligen
int Wert finden wir beispielsweise in der Konstante
INT_MIN. Die Maximalwerte in
INT_MAX bzw. für unsigned in
UINT_MAX. In Java und C# gibt es für jeden primitiven Datentyp eine zugehörige Klasse, in der wir solche Informationen finden – genannt
„Wrapperklasse“. In C# heißt diese Wrapperklasse genauso wie der primitive Datentyp. Java folgt seinen internen Namensregeln und dort wird
sie entsprechend in Großbuchstaben benannt:
| Datentyp: | Wrapperklasse: |
|---|---|
| byte | Byte |
| short | Short |
| int | Integer |
| long | Long |
| boolean | Boolean |
| char | Character |
Tabelle 5: Wrapperklassen in Java
Wenn wir in Java also einer
long Variablen den Maximalwert zuweisen möchten, so schreiben wir:
Listing 22: Zugriff auf Wrapperklassen in Java
In C# würde dies der folgende Code erledigen:
Listing 23: Zugriff auf Wrapperklassen in C#
Die Wrapperklassen haben übrigens noch einen weiteren Daseinsgrund. In Java und C# ist alles in Klassen verpackt – auch die grundlegenden
Funktionalitäten die wir bspw. für ganze Zahlen oftmals benötigen. Ein Beispiel hierfür wäre die Umwandlung eines Strings in eine
int Zahl – was wir später noch ansehen werden.

Umwandlungen und Typecasts
Den letzten Punkt zum Thema „primitive Datentypen“ ist der sogenannte „Typecast“. Hierunter versteht man das Übernehmen eines Wertes von
Datentyp A in eine Variable des Datentyps B – also beispielsweise wollen wir den Inhalt einer
„short“ Variablen in eine
„int“ Variable eintragen. Hierbei gibt es nun zwei Fälle. Im ersten Fall übergeben wir die Daten von der Variablen eines Datentyps, in die
Variable eines anderen Datentyps mit einem kleineren Wertebereich und im anderen Fall eben umgekehrt:

Abb.: 15: Datentransfer (Typecast) über unterschiedliche Datentypen
Es sollte nachvollziehbar sein, dass wir bei der Übertragung von einem „großen“ Datentyp in einen „kleinen“ Datentyp in Gefahr laufen,
Informationen zu verlieren. Probieren wir es mal mit der Programmiersprache aus, die am unkritischsten mit Datentypkonversionen umgeht, nämlich C:
Listing 24: Datenverlust durch falsche Datentypen in C
Kurze Erklärung der Codezeilen: Wir erzeugen eine Variable
„i“ vom Typ
int, welche einen Wertebereich von -2.147.483.648 bis 2.147.483.647 hat. Der Wert 32.768 passt also dort hinein. Danach schreiben wir den
Wert von dort in eine
short Variable
„s“, welche den Wertebereich von -32.768 bis 32.767 aufweist. Die Zahl in der int Variable „i“ passt also nicht in die short Variable.
Wenn wir das Programm ausführen, sehen wir:
auf der Konsole. Um dieses Verhalten zu verstehen, sehen wir uns einfach die Bits der beiden Zahlen an:
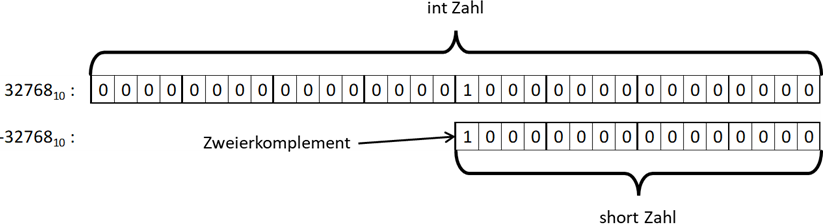
Abb.: 16: Bitmuster bei Übernahme der Zahl 32.768 von int nach short
int hat eine Breite von 32 Bit,
short „nur“ 16. Wenn die Bits 1:1 übernommen werden, so werden die Bits 1:1 kopiert und der linke „Überhang“ abgeschnitten. Nun ist aber im
Zieldatentyp das linke Bit gesetzt, wodurch wir eine Interpretation als Zweierkomplement durchführen müssen, was entsprechend zur -32.768
führt. Wir haben also einen Datenverlust erlitten. Dieser ist aber nur dann zu beklagen, wenn der Wert in einer int Variablen nicht in die
short Variable hineinpasst. Man kann es sich vorstellen, wie Wasser in einem großen ½ Liter Glas, das wir in ein kleineres ¼ Liter Glas
schütten. Nun muss das große Glas aber nicht voll sein. Nur wenn der Inhalt somit im großen Glas kleiner oder gleich ¼ Liter ist, haben wir
kein Problem.
Wie sieht es mit den Gleitkommazahlen in Verbindung mit ganzen Zahlen aus? Hier gibt es zwei Dimensionen der „Ungenauigkeit“, und zwar die
offensichtliche Problematik, dass Nachkommastellen in ganzzahligen Datentypen nicht abgebildet werden können und die Anzahl der signifikanten
Mantissenziffern. Beginnen wir mit letzterem:
Listing 25: Datenverlust durch falsche Datentypen in C
Die Ausgabe ist:
Wie die Angabe in Tabelle 3 schon andeutet, haben wir nur 7 signifikante Mantissenziffern bei der Ausgabe. Unser Ergebnis ist also nur auf
die ersten 7 Stellen genau. In solchen Fällen sollten wir dann natürlich auf
„double“ zurückgreifen. Wie sieht es andersherum aus? Probieren wir es aus:
Listing 26: Datenverlust durch falsche Datentypen in C
Aufgrund der Anzahl der signifikanten Stellen haben also auch hier die gleiche Ungenauigkeit wie bei Übernahme von
int nach
float. Analysieren wir nun mal den Umgang mit Nachkommastellen:
Listing 27: Datenverlust durch falsche Datentypen in C
Die Nachkommastellen werden also einfach „abgeschnitten“. Sie werden nicht gerundet! Das mag einem Mathematiker vielleicht jetzt
verwunderlich erscheinen, aus Computersicht ist dies aber die einzig richtige Verhaltensweise. Das „Runden“ ist eine zwar nachvollziehbare
aber trotzdem willkürliche Definition. Eine Kommazahl besteht nun mal aus einem ganzzahligen Teil und den Nachkommastellen…und der
ganzzahlige Teil ist genau das, was wir in einer Variablen für ganze Zahlen erwarten.
Einen ganzzahligen Datentyp kennen wir noch – den Typ
„char“. Auch wenn er für das Speichern von Zeichen genutzt wird; die eigentlich gespeicherten Werte sind nun mal Zahlen. Dies können wir
durch einen sehr einfachen Code beweisen:
Listing 28: Datenverlust char als Zahlwert in C
Kurze Erklärung der Codezeilen: Wir erzeugen eine
char Variable
„c“ und schreiben ein Zeichen (in unserem Fall den Wert 'a') hinein. Dann geben wir den Variableninhalt als Zahl
(„%d“) und als Zeichen
(„%c“) aus. Danach belegen wir c mit einer int Zahl (Zahlenkonstanten sind in C immer vom Typ
int) und geben sie wieder als Zahl und Zeichen aus.
Die Ausgabe lautet:
Im Prinzip ist die Erkenntnis hier die gleiche wie in
Listing 20, nur dass wir jetzt wissen, was da eigentlich passiert. Das ist insofern wichtig, als
dass wir bspw. jetzt auch folgenden Code interpretieren können:
Listing 29: Negative int Werte als Zahlwert in C
Kurze Erklärung der Codezeilen: Der Code soll demonstrieren, wie C mit einer Negativen Zahl umgeht. Das Einfachste wäre nun,
einfach eine negative Zahl (bspw. -191) zuzuweisen. Einige C-Compiler prüfen jedoch die Zuweisung auf Plausibilität und
da
char Variablen keine Negativen Werte aufnehmen können, würde hier ein Compilerfehler
entstehen. Insofern weisen wir einfach die 191 zu und multiplizieren den Wert in c mit der -1 und weisen das Ergebnis
einfach wieder der Variablen c zu:
c = c * -1;
Hier die Ausgabe:
Die Bitkombination von -191 sind in den linken 3 Bytes nur Einsen – aufgrund des Zweierkomplements. Das letzte Byte trägt die Kombination
0100.00002.
char wiederum nutzt in C nur ein Byte, weshalb nur diese Bitkombination gewertet wird, was wiederum die 65 und somit das Zeichen „a“ ist.
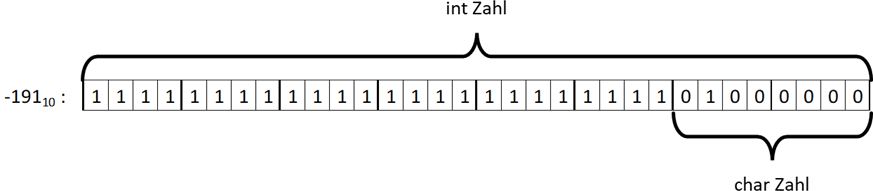
Abb.: 17: Bitkombination von -191 als int und char (in C)
Das Ganze gilt jedoch nur für C, da dort
char mit einem Byte dargestellt wird. In Java oder C# werden
char Daten als UTF16 mit zwei Bytes codiert. Dies ist übrigens nicht der einzige Unterschied zwischen Java/C# zu C. Insofern sehen wir
uns mal grundsätzlich an, was bspw. Java mit solchen Zuweisungen macht. Beginnen wir mit der Zuweisung eines „kleinen“ Datentyps auf
einen „großen“:
Listing 30: Impliziter Typecast in Java
Wie in C auch, funktioniert das problemlos. Drehen wir nun das Ganze um:
Listing 31: Fehlender expliziter Typecast in Java
Wer versucht, diesen Code zu kompilieren wird enttäuscht werden – wir haben hier einen Syntaxfehler! Java akzeptiert die Zuweisung
eines „großen“ Datentypen auf einen „kleinen“ nicht, da hier Datenverlust droht. Trotzdem kann man Java dazu bewegen, diese Zuweisung
doch zu akzeptieren, indem wir vor
„i“ in Klammern den Zieldatentyp (in unserem Fall
„short“) schreiben:
Listing 32: Expliziter Typecast in Java
Jetzt kompiliert der Code und wir bekommen auch den richtigen Wert „10“ auf der Konsole. Damit haben wir den Code für zwei wichtige
Begriffe kennengelernt – impliziter und expliziter Typecast:
expliziter Typecast: Umwandlung eines Wertes von einem in einen anderen Datentyp mit einem expliziten Hinweis, dass diese
Umwandlung durchgeführt werden muss. Bei den meisten Programmiersprachen wird der Zieldatentyp in Klammern vor der Quelle
(in unserem Fall die umzuwandelnde Variable) geschrieben.
impliziter Typecast: Umwandlung eines Wertes von einem in einen anderen Datentyp, ohne dass im Programm diese Umwandlung
angegeben wird.
Was bei einem expliziten Typecast eigentlich passiert ist, dass nur für die Dauer der Operation (in unserem Fall ist dies die
Zuweisung mit
„=“) der Wert umgewandelt wird. Wenn im Code also steht
„short s = (short) i;“ wird der Wert aus i ausgelesen, als short uminterpretiert und dann zugewiesen.
Die Faustregel in Java und C# lautet – immer dann, wenn Datenverlust aufgrund Typumwandlungen drohen, fordert der Compiler einen
expliziten Typecast ein. Grundsätzlich empfehle ich, diese Faustregel auch in C zu verwenden, obwohl sie hier nicht zwingend erforderlich ist.
Es gibt allerdings einen Fall, bei dem diese Faustregel nicht gilt. Sehen wir uns folgenden C# Code an:
Listing 33: Impliziter Typecast mit Datenverlust in C#
Hier benötigt der Compiler keinen Typecast. Der Wertebereich von
float ist ja weitaus größer als der von
int, allerdings nicht die Genauigkeit – sprich die Anzahl der signifikanten Stellen. Wenn wir das Programm starten, sehen wir:
Mit anderen Worten, wir haben keinen expliziten Typecast benötigt, haben aber trotzdem einen Datenverlust erlitten. Wenn wir allerdings
mit den Standarddatentypen für Gleitkommazahlen
(double) und Ganzzahlen
(int) arbeiten, tritt dieses Problem nicht auf, da die Genauigkeit von
double für
int ausreichend ist.
Gehen wir nun am Schluss nochmal auf die Eigenheiten von
char in C# und Java ein. In beiden Programmiersprachen haben wir einen (Zahlen-)Wertebereich bei
char von 0 bis 65.535, da wir die Werte auf 16 Bit ohne Vorzeichen speichern. Insofern können wir nicht mit -191 das „A“ provozieren,
sondern mit -65.471.
Listing 34: Typecast bei char in C#
Der Wert -65.471 hat als Bitmuster 1111.1111.1111.1111.0000.0000.0100.00012, wodurch die rechten 16 Bit
wieder den Wert 65 für „A“ ergeben. Der letzte zu prüfende Typecast dreht sich um
boolean. Da C und C++ diesen Datentypen einfach aus einer Zahl generieren dürfte klar sein, dass wir hier Zahlenwerte direkt in
bool „casten“ können:
Listing 35: Typecast int nach bool in C bzw. C++
Da in C hinter den Boolean Werten Zahlen stehen dürfte es nicht wundern, dass der Typecast implizit möglich ist. Überraschend ist vielleicht,
dass dies anstatt mit
int auch mit
double funktionieren würde, wobei dies keine praktische Relevanz hat. In C# bzw. Java ist dies aufgrund der sauberen Trennung von
Zahlendatentypen und
boolean nicht möglich – wir würden sowohl bei einem impliziten, als auch einem expliziten Typecast einen Compilerfehler erhalten.
Wir merken uns also, dass wir nicht beliebig die Werte von einem Datentyp in den anderen umwandeln können. Es kommt zwar nicht so
häufig vor, aber wenn es mal notwendig ist, sollte uns immer klar sein, was wir da eigentlich machen.

CC Lizenz (BY NC SA)
