Funktionales Programmieren - der akademische Weg
Ich muss gestehen, dass ich relativ lange darüber nachgedacht habe, ob ich dieses Kapitel überhaupt mit in das Buch einfügen soll. Für Programmiereinsteiger ist das funktionale Programmierparadigma
eine ziemlich harte Nuss, da es an vielen Stellen recht abstrakt wirkt. Wer sich schon mal mit diesem Thema mittels einschlägiger Literatur oder auch Tutorials beschäftigt hat wird erstmal den Gedanken nicht los,
dass man hier eher das Problem zur Lösung sucht, und nicht umgekehrt – die engagierten funktionalen Programmierer mögen mit diesen Satz verzeihen...

Grundideen funktionaler Programmierung
Aber worum geht es eigentlich bei der funktionalen Programmierung? Nun, während wir bei der objektorientierten Programmierung in erster Linie versuchen die Programmierwelt an die uns umgebene Welt anzulehnen,
ist die Zielsetzung der funktionalen Programmierung eher, sie an die mathematische Welt zu orientieren. Daher auch der Name „funktional“ – er lehnt sich weniger an den Funktionsbegriff aus der Informatik des
Kapitels 8 an, sondern vielmehr an den Funktionsgedanken der Mathematik. Streng genommen ist die funktionale Programmierung das exakte Gegenteil der objektorientierten Vorgehensweise (wobei
von der Definition her das Gegenstück zur funktionalen Programmierung die imperative Programmierung ist). War die Innovation bei Objekten, dass wir hier Funktionalität und Daten in einem Konstrukt vereinen, trennt
die funktionale Programmierung diese beiden Dinge schon fast dogmatisch. Eine „pure“, oder „reine“ Funktion wird immer das gleiche Verhalten bezüglich der Eingangsdaten zeigen – egal wie oft man sie aufruft.
Wenn wir uns an den Getränkeautomaten aus
Kapitel 13 erinnern, war das hier aber das eigentliche Problem! Hier haben wir extra eine Variable für die Speicherung der Getränkedosen eingeführt, damit sich die Simulation des Automaten sich möglichst wie ein echter
Automat verhält. Bei der funktionalen Programmierung möchte man dies unter allen Umständen verhindern. Man spricht hier von zu vermeidenden „Seiteneffekten“ – also die Veränderung der Gesamtsituation durch einen
Funktionsaufruf. Aber wie kann man mit dieser Einschränkung überhaupt etwas bewerkstelligen? Hier möchte ich nochmal die Mathematik bemühen. Gehen wir mal von einer einfachen Funktion aus – sagen wir eine Geradenfunktion:
f(x) = 2x + 3
Wir finden hier eine Eingangsvariable x, welche ein Ergebnis liefert. Auf einem Koordinatensystem wäre dies der y – Wert. Egal wie oft wir ein x (sagen wir mal x = 3) einsetzen, wir werden immer als Ergebnis die 9
erhalten. Ein weiteres auffälliges Verhalten ist, dass wir streng genommen die 9 sofort erhalten. Es wird nicht groß iteriert oder irgendwelche anderen sequenziellen Verarbeitungen durchgeführt – das Ergebnis steht
eigentlich in 0 Sekunden fest. Wir haben auch keinen Wert verändert – wir haben aber einen neuen geschaffen – nämlich y = 9. Und dies wird bei funktionalen Programmiersprachen auch bis zum Exzess durchgehalten.
Wenn bei einer reinen funktionalen Programmiersprache ein Array übergeben wird, um dieses bspw. zu sortieren, erhalten wir immer ein neues Array zurück – alle Variablen sind also immutable („unveränderbar“).
Das geht soweit, dass man weitestgehend auch auf Zuweisungen verzichtet – schließlich ändert eine Zuweisung ja den Wert einer Variablen. Um nun doch sowas wie Funktionalität zu erhalten, werden nun Funktionen
ineinander verschachtelt. Funktionsergebnisse werden direkt als Parameter von Funktionen verwendet – zum nicht unerheblichen Teil auch rekursiv. Sehen wir uns also in JavaScript mal einen Zähler imperativ und funktional an:
Listing 1: Zählschleife imperativ
Rufen wir die Funktion mit dem Wert 10 aus, wird die Ausgabe die Zahlenreihe von 1 bis 10 sein. Wir haben hier zwei Zuweisungen in unserem Code. Die Variable
i wird auf 1 gesetzt und um 1 erhöht. Sehen wir uns das Ganze nun funktional an:
Listing 2: Zählschleife "funktional"
Kurze Erklärung der Codezeilen: Die Funktion wird ebenfalls mit einem Parameter aufgerufen. Danach wird geprüft, ob der Parameter über 0 ist, da nur dann die Funktion ausgeführt werden darf.
Ist dies der Fall, ruft sich die Funktion rekursiv selbst auf, allerdings mit einem neuen Parameter, welcher einfach um eins kleiner als der ursprüngliche Parameter ist. Danach wird der Parameter
einfach ausgegeben. Würden wir die Ausgabe und den rekursiven Aufruf tauschen, hätten wir einen Rückwärtszähler.
Wir erhalten mit dem funktionalen Code exakt das gleiche Ergebnis wie der imperative Ansatz, allerdings ohne irgendeine Zuweisung genutzt zu haben. Ob das nun sinnvoll ist oder nicht sei mal dahingestellt.
Entscheidend ist erstmal, dass es funktioniert. Der pure funktionale Programmierer würde allerdings bei unserem funktionalen Zähleransatz ebenfalls die Nase rümpfen und sagen, dass wir trotzdem einen
Seiteneffekt in unserer Funktion haben – nämlich die Ausgabe. Seine Empfehlung wäre nun, die Ausgabe als Funktion wiederum als Parameter mitzugeben. Also eine Funktion als Parameter, welche sich
um die Ausgabe kümmert. Damit ist diese Bürde von unserem eigentlichen Zähler genommen und er wäre dann „sauber“. An diesem kleinen Beispiel können wir nun erahnen, was bei der funktionalen Programmierung
auf uns zukommt. Dadurch, dass wir die Werte nie irgendwo ablegen, sondern immer als neuen Parameter an tiefer verschachtelte Funktionen weitergeben, kann man sich das funktionale Programmieren wie jonglieren
vorstellen. Man muss immer alle Bälle in der Luft halten – sprich merken, welche Funktion gerade welchen Wert von einer darüberliegenden Funktion erhält. Beim imperativen Programmieren hingegen kann man immer
mal zwischendurch einen „Ball“ in einer Variablen ablegen und später wieder aufnehmen. Nun wäre es vermessen zu versuchen, die Welt der funktionalen Programmierung in einem Kapitel eines allgemeinen
Programmierbuches abzuhandeln. Vielmehr möchte ich hier die Grundgedanken aufbereiten, in einen sinnvollen Kontext bringen und funktionale Ansätze als Ergänzung von imperativen Programmen zu verstehen.
Wir werden deshalb auch nicht mit einer reinen funktionalen Programmiersprache arbeiten – wie bspw. Haskell oder F#, sondern aus unserem bekannten Sammelsurium von Programmiersprachen einfach eine geeignete
nehmen und mit dieser dann loslegen. Hierbei werden wir auf ein paar funktionale Dogmen verzichten (bspw. die Unveränderbarkeit aller Variablen). Trotzdem soll das Wesen der funktionalen Ansätze herausgearbeitet
werden. Prinzipiell können wir mit den meisten der hier behandelten Sprachen arbeiten, die Skriptsprachen eigenen sich aber am meisten, da sie Funktionen höherer Ordnung relativ gut ermöglichen. Funktionen
höherer Ordnung sind Funktionen, welche nicht einen Wert als Parameter erwarten bzw. zurückgeben, sondern ganze Funktionen. Dies wird durch das bereits besprochene Konzept der Zuweisung von Funktionen auf
eine Variable ermöglicht („Function as first class citicens“). Am geeignetsten stechen hier JavaScript und Python heraus. Da wir beim Multitasking etwas intensiver mit JavaScript gearbeitet haben, nehme ich
für dieses Kapitel zur Abwechslung einfach Python.
Nun stellt sich aber vor dem Hintergrund der auf den ersten Blick undurchsichtigen Programmerweise noch die zwingende Frage, warum das alles? Nun zum einen ist hier zwar aller Anfang schwer, aber wenn man
sich an die grundsätzliche Denkweise gewöhnt hat, kommt einem der funktionale Ansatz nicht mehr ganz so ungewöhnlich vor. Die wahren Vorteile liegen jedoch in der einfachen automatischen Testbarkeit funktionaler
Ansätze (und hier spreche ich explizit nicht vom Debuggen, sondern vom testgetriebenen Entwicklungsansatz – siehe nächstes Kapitel) und von der einfachen Skalier- und Parallelisierbarkeit. Durch die
fehlenden Seiteneffekte können die einzelnen Aufrufe der Funktionen abwechselnd von unterschiedlichen Threads – ja sogar unterschiedlichen Rechnern abgearbeitet werden. Gerade bei der hochskalierbaren Serverwelt
ein unschätzbarer Vorteil. Und genau deshalb ist es erstmal nicht wichtig rein funktional zu programmieren, sondern die Ansätze vom Prinzip her zu verstehen und sie auch bei imperativen Programmen einzusetzen.
Gehen wir nun nochmal auf unser Beispiel des Zählers ein. Wir haben hier einen Wert immer wieder verändert und als Parameter rekursiv in einen weiteren Funktionsaufruf gesteckt. Das Konzept, das
Funktionsergebnis als Parameter in eine weitere Funktion zu schreiben ist nun nichts neues, da wir es bisher ja in einigen anderen Stellen ja auch bereits durchgeführt haben. Bspw. wenn wir in
Python eine Stringausgabe machen wollen, wobei wir hier alles gerne in Großbuchstaben hätten:
print(myString.upper()); Hier ist dies einfach eine Umsetzungsvariante für „Schreibfaule“ – wir könnten ja auch die Großbuchstaben in einer Zwischenvariablen ablegen und diese dann ausgeben.
Bei funktionalen Ansätzen wird die kompakte Schreibweise jedoch zu einem Grundprinzip erhoben. Man versucht hier diese Kompaktheit, wenn es irgendwie geht, umzusetzen. Dies kommt wiederum von der
Vorgabe, möglichst keine Zuweisungen durchzuführen. Wir wollen bzw. sollen hier also nicht die Großbuchstabenwerte in einer Variablen zwischenspeichern und dann ausgeben, sondern dies in einem
Schritt ohne die Zwischenvariable realisieren. Im Idealfall verarbeiten die Funktionen zu allem Überfluss auch immer nur einen Wert. In unserem Zählerbeispiel aus
Listing 2 hat die Funktion
doCountFunc() auch nur einen Parameter. Dies scheint nun eine weitere, auf den ersten Blick extrem restriktive Einschränkung zu sein! Hierfür werden wir aber gleich einen Lösungsansatz finden.
Gehen wir nun mal davon aus, dass wir eine Funktion haben wollen, welche eine Zahl quadriert:
Listing 3: Quadratfunktion in Python
Der Aufruf
print(sq(3)) ergibt nun die 9 auf der Konsole. Was ist aber nun, wenn wir eine Liste von Zahlen haben, welche alle quadriert werden müssen. Eine Lösung wäre nun:
Listing 4: sq() Anwendung auf eine Liste in Python
Das Ganze ist nun nicht wirklich kompakt und schon gar nicht funktional, da wir wieder Zuweisungen haben. Um solche Funktionalitäten nun umsetzen zu können, finden wir bei allen
Programmiersprachen, welche funktionale Ansätze unterstützen die „map“ Funktion. Sie wendet einfach auf jeden Wert einer Liste eine zu übergebende Funktion an. Dies bedingt aber,
dass wir in der Lage sein müssen, Funktionen als Parameter übergeben zu können:
Listing 5: sq() Anwendung auf eine Liste mittels map()
Kurze Erklärung der Codezeilen:
listIn beinhaltet wieder die Liste von Zahlen. Die Funktion
map() erwartet nun zwei Parameter, einmal die anzuwendende Funktion
sq und die abzuarbeitende Liste. Als Rückgabewert liefert
map() ein
map Objekt, welches wiederum über
list() zu einer Liste umgewandelt wird.
Die Ausgabe des Codes aus
Listing 4 und
Listing 5 sind identisch. Der Verfechter der funktionalen Programmierung wird nun sagen – seht her, die Lösung ist super kurz und elegant! Der Zweifler wiederum mag nun einwenden, ja – schon richtig,
aber das sieht sehr nach einer Lösung für ein Problem aus, das ich noch nie hatte! Nun ist es müßig darüber nachzudenken, ob dies nun sinnvoll ist oder nicht – wichtig ist, wir haben einen weiteren
Baustein in unserem Programmierwerkzeugkasten, den wir bei Bedarf verwenden können. Nun ist es auch möglich, die Definition der Quadrierungsfunktion anonym zu gestalten. Wenn wir die Quadrierung wirklich
nur an einer Stelle benötigen, so bietet sich dies an. Python erlaubt eine solche Definition mittels des
lambda Schlüsselwortes:
Listing 6: map() mit anonymer Funktion
Kurze Erklärung der Codezeilen: Der
lambda Operator erwartet nun den Parameter – in unserem Fall
x und im Anschluss nach dem Doppelpunkt die Rechenvorschrift – die Quadrierung.
Auch hier erhalten wir wieder das gleiche Ergebnis.

Funktionen auf Listen anwenden
Wir haben die Tür in die funktionale Programmierung nun einen kleinen Spalt aufgestoßen. Nun wollen wir uns mit den Problemstellungen der
restriktiven Regeln etwas auseinandersetzen. Gehen wir nun davon aus, wir wollen eine weitere Funktion über
map() anwenden. Und zwar soll diese Funktion jeden Wert der Liste mit einem weiteren Parameter multiplizieren. Die Funktion soll
multWith() heißen:
Listing 7: Funktion zur Mutliplikation
Wenn wir nun jeden Wert der Liste mit – sagen wir mal 2 – multiplizieren wollen, haben wir nun ein Problem. Mittels
map() auf eine Liste angewendet erhalten wir pro Element ja immer nur einen Wert. Wir brauchen aber zwei für unsere
multWith() Funktion. Dieses Problem können wir nun mit Hilfe von Closures lösen. Ein Closure ist ein Funktionskontext, in der Werte definiert werden, welche in einer untergeordneten Funktion genutzt werden.
Sehen wir uns hierfür ein abstraktes Beispiel an:
Listing 8: Beispiel für Closure in Python
Kurze Erklärung der Codezeilen: Die
outerFunction() bildet ein Closure, welches die
innerVar und die
innerFunction() beinhaltet. Die
innerFunction() läuft also im Kontext der
outerFunction(). Da wir in der
outerFunction() den Wert der
innerVar auf 3 setzen, wird dieser Wert in der
innerFunction() verwendet. Beim Aufruf des Konstruktes mit dem Wert 4 wird somit 3*4 = 12 gerechnet und ausge-geben.
Nun gehen wir einen Schritt weiter und geben der
outerFunction() zwei Parameter, von denen einer über die Parameterliste an die innere Funktion übergeben wird und ein zweiter als gebundene Variable im Closure:
Listing 9: Beispiel für Closure in Python mit zwei Parametern
Kurze Erklärung der Codezeilen: Das Beispiel funktioniert genauso wie das aus
Listing 8, lediglich wird die Variable
b, welche im Kontext behandelt wird aus der Parameterliste von
outerFunction() genommen.
Nun setzen wir das Ganze noch mit Hilfe einer anonymen Funktion um:
Listing 10: Beispiel für Closure in Python mit zwei Parametern
Kurze Erklärung der Codezeilen: Die Multiplikation wird nun mit
(lambda x: x * b) durchgeführt.
x ist hierbei der Parameter der Funktion, welcher mit
(a) belegt wird. Somit haben wir als Ausgabe wieder die 12.
Hiermit haben wir nun die Bedingungen geschaffen, um unser
multWith() Beispiel zu realisieren:
Listing 11: Multiplikation aller Listeneinträge mit Wert
Kurze Erklärung der Codezeilen: Die
lambda anonyme Funktionsdefinition wird hier benötigt, da wir eine lokale Funktion brauchen, welche zusammen mit der Variable
b ein Closure bildet. Somit existiert
b im Funktionsaufruf von
multWith(). Die anonyme Funktion hat jedoch nur noch einen Parameter (das
x) welches wiederum auf die Listenelemente angewendet wird.
Die Ausgabe ist entsprechend 4, 8 und 16. Da wir hier nun ohnehin eine anonyme Funktionsdefinition im
map() Aufruf haben, können wir diese gleich als Multiplikation formulieren und den Aufruf
multWith() komplett weglassen:
Listing 12: Multiplikation aller Listeneinträge mit Wert ohne inneren Funktionsaufruf
Damit haben wir den Code erheblich reduziert.

Curryfizieren
In diesem Zusammenhang können wir uns noch eine weitere Besonderheit bei funktionalen Programmieransätzen ansehen –
das „Curryfizieren“ oder englisch „currying“. Der Name kommt von einem Herrn Haskell Brooks Curry, der als Mathematiker einige wissenschaftliche Grundsteine gelegt hat,
welche essenziell für die funktionale Programmierung sind. Die Idee hinter Curryfizieren ist, dass man Funktionen mit mehreren Parametern in eine Kaskade von Funktionen
mit je einem Parameter umwandelt. Also eine Funktion f(a, b, c) wird zu f(a)(b)(c). Dies ist in den Programmiersprachen nur dann möglich, wenn wir Funktionen als
Rückgabewert von Funktionen definieren können. Sehen wir uns das mal in einem Beispiel an, indem wir die Multiplikation aus
Listing 7 als currifizierte Funktion schreiben:
Listing 13: Curryfizierung einer Funktion mit zwei Parametern
Kurze Erklärung der Codezeilen: Die Funktion
mult() erwartet als Parameter die Variable
x. Diese wird als Closure zusammen mit der anonymen Funktion
lambda a: x * a zusammengefasst. Die Anonyme Lambda Funktion erwartet einen Parameter
x und wird von der
mult() Funktion zurückgegeben. Es wäre somit möglich,
tmpFunc = mult(2) zu schreiben.
tmpFunc würde also auf die anonyme Funktion verweisen und könnte mit
tmpFunc(4) aufgerufen werden. Diesen Schritt kann man jedoch zusammenfassen, indem man
mult(2)(4) schreibt.
Grafisch kann man sich diese Situation wie folgt vorstellen:

Abb.: 1: Aufrufstruktur beim Currifizieren / direkter Call und „Umweg“ über tempFunc Variablenzuweisung
Die Ausgabe wäre 8. Mit diesem Konzept könnten wir nun auch die Multiplikation aller Werte einer Liste realisieren:
Listing 14: Multiplikation aller Listeneinträge mit Wert ohne inneren Funktionsaufruf
Kurze Erklärung der Codezeilen: Die Funktion
mult() wird nun mit dem Closure
b aufgerufen. Der Rückgabewert von
mult() ist aber nun eine Funktion mit einem Parameter, der wiederum auf die Werte der Liste gemappt werden kann, weshalb wir
mult(b) als Parameter für
map() verwenden können.

Abb.: 2: Anwendung der rückgegebenen Lambdafunktion auf die Listenelemente via map()

Filterfunktion
Eine weitere Funktionalität, welche wir auf Listen anwenden können, ist die Filterfunktion. Hierbei wird eine Liste verarbeitet und jedes Element mittels einer Bedingung auf eine Eigenschaft hin überprüft.
Wenn das Element die Eigenschaft erfüllt, wird es in die Ausgabeliste übernommen, ansonsten entfernt. Sehen wir uns diese Funktionalität mal in einem einfachen Beispiel an, welches aus einer Liste alle
geraden Zahlen übernimmt und alle ungeraden entfernt:
Listing 15: Entfernen ungerade Zahlen aus Liste
Kurze Erklärung der Codezeilen: Die Funktion
checkEven() prüft
x daraufhin, ob der Wert gerade ist. Wenn ja, wird er zurückgegeben, ansonsten passiert nichts. Mit
filter() kann nun diese Funktion auf alle Elemente angewendet werden, was somit nur noch die geraden Elemente in der Rückgabeliste belässt.
Die Ausgabe ist hier nun 2, 4 und 6. Diese Funktionalität kann man nun noch etwas verkürzen, indem man die Filterregel in eine anonyme Funktion verbannt:
Listing 16: Entfernen ungerade Zahlen aus Liste
Kurze Erklärung der Codezeilen: In der anonymen Funktion muss nun kein Rückgabewert mehr definiert werden, sondern lediglich die Filterbedingung. Den Code aus der
checkEven() Funktion könnten wir in Python ohnehin nicht in die
lambda Funktion einbetten, da wir hier keine Zeilenumbrüche durchführen können. Diese waren in Python ja Strukturelemente (wie die geschweiften Klammern und Semikolons in den anderen Sprachen).
Mit diesem Wissen können wir nun endlich eine Funktionalität funktional realisieren, welche wir in
Kapitel 17 imperativ realisiert haben – die Primzahlenermittlung mit Hilfe des Siebs des Eratosthenes. Die Idee hier war ja, dass wir in einer Liste von Zahlen die Primzahlen markieren wollten.
In der imperativen Lösung haben wir hierzu ein Array von
boolean Werten erzeugt, bei dem die Position den Wert bestimmt und der Inhalt
true auf eine Primzahl hinweist. Hierzu haben wir alle „nicht-Primzahlen“ mit
false markiert. Danach haben wir alle mit
true geflaggten Positionen als Wert in ein neues Array übertragen. Funktional können wir diesen Algorithmus nun eleganter erledigen, da wir nun die
filter() Funktion haben, womit wir einfach die „nicht-Primzahlen“ aus dem Array herauslöschen können – wir flaggen die Werte also nicht mit
false, sondern nehmen sie komplett raus. Dadurch ist die Position im Array nun nicht mehr mit dem Wert gleichzusetzen, weshalb wir kein
boolean Array mehr verwenden können, sondern ein
int Array, in dem initial alle Zahlen von 2 bis zur Obergrenze eingetragen werden. Dieses Array wird dann (Prim-)Zahl für (Prim-)Zahl durchgearbeitet. Die zu prüfenden Primzahlen entnehmen wir wieder dem Array – so wie beim imperativen Ansatz auch

Abb.: 3: Entfernen der nicht-Primzahlen
Wir sehen in der Abbildung, dass wir mit der vordersten Zahl, der 2 als kleinste Primzahl beginnen. Mit jedem neuen Durchlauf nehmen wir den nächsten Wert, was zwingend immer eine Primzahl sein muss – 3, dann 5, dann 7 usw., da die
nicht-Primzahlen ja fortlaufend rausgenommen werden. Neben der geänderten Arraystruktur benötigen wir noch eine zweite wesentliche Änderung im Vergleich zum imperativen Ansatz. Wir müssen eine Filterregel formulieren. Da wir die
Elemente entfernen, kann die Identifikation der nicht-Primzahlen ja nicht durch die Addition von Werten erfolgen, sondern muss über eine Teilbarkeitsprüfung – sprich modulo – erfolgen. Wir benötigen also eine Funktion, welche prüft, ob zwei Werte voneinander teilbar sind:
Abb.: 4: Prüfung auf Primzahl
Hierbei müssen wir darauf achten, dass bei der Prüfung der Inhalt von x auch gleich der Prüfzahl d sein kann – jedoch dann die Modulorechnung fälschicherweise auch 0 ergeben würde. Dies ist deshalb notwendig, da
filter() immer die gesamte Liste prüft – also wird bspw. bei der Prüfung auf Divisor = 2 auch immer die 2 selbst getestet, da 2 ja als Primzahl in der Liste vorhanden sein muss. Nun fehlt noch die Abbruchbedingung.
Wir sind wie in
Kapitel 17 auch hier am Ende der Prüfung angelangt, wenn der Divisor 2 größer als die Wurzel des maximalen Wertes geworden ist. Somit haben wir alle Puzzleteile für
unseren Algorithmus beisammen und können ihn programmieren:
Listing 17: Sieb des Eratosthenes funktional
Kurze Erklärung der Codezeilen: Da wir die Prüfgrenze über die Wurzel ermitteln, müssen wir
math importieren. Danach schreiben wir den Filter, welcher entsprechend
Abbildung 4 umgesetzt wurde. Der eigentliche Sieb benötigt eine wiederholte Anwendung des Filters, wodurch wir – streng nach funktionalen Vorgaben – eine rekursiv aufrufbare Funktion
sieb() erstellen. Diese benötigt die zu verarbeitende Liste
l, die Position
p in der Liste, aus der die Primzahl für die Filterprüfung entnommen wird (also die grau markierten Felder in
Abbildung 4) und die maximale Zahl
m, mit der wir den Filter laufen lassen – was die Wurzel des maximalen Wertes in der Liste ist. In der
sieb() Funktion prüfen wir erstmal, ob wir überhaupt weitermachen müssen – sprich ob die aktuell prüfende Primzahl
l[p] kleiner gleich der Obergrenze ist. Wenn wir nicht über der Obergrenze sind, rufen wir
sieb() wieder auf – diesmal aber mit einer gefilterten Liste. Wir wenden also den Filter auf die Liste an – mit der Prüfzahl auf Position
p. Dies muss aufgrund des zweiten Parameters von
primeFilter() mit einem Closure durchgeführt werden. Im ersten Durchlauf wird nun die Position die 0 sein – also die Zahl auf dem vordersten Listenfeld, die 2. Im ersten Rekursiven Aufruf wird also eine Liste übergeben,
in der alle Vielfachen von 2 herausgenommen wurden. Damit im ersten Rekursiven Aufruf nun die nächste Primzahl verwendet wird, zählen wir die Position um eins hoch
(p + 1), wodurch die 3 als nächste Prüfzahl verwendet wird. Dies wird also solange wiederholt, bis unsere Prüfzahl größer dem Maximalwert ist. In diesem Fall wird die aktuelle Liste einfach zurückgegeben. Beim initialen Aufruf von
sieb() müssen wir nun eine Liste von Zahlen übergeben, welche bei 2 anfängt und bis zum Maximalwert
maxVal geht. Hier addieren wir bei
range() noch eins dazu, da
range() die Werte bis exklusive der rechten Grenze erzeugt.
Lassen wir den Code laufen, sehen wir die Primzahlen bis inklusive 2000. An dem Code aus
Listing 17 sehen wir nun, dass funktionale Programme recht kurz ausfallen. Für den ungeübten (funktionalen)
Programmierer ist diese Kompaktheit jedoch nicht wirklich einfach zu durchdringen. Ein weiteres nicht zu unterschätzendes Problem ist, dass der Code durch die Rekursion nicht performant ist. Die imperative
Umsetzung des Siebs von Eratosthenes ist ungleich schneller als die hier präsentierte Lösung.

Reduktion von Listen
Die nächste, für funktionale Programmierung wichtige Funktionalität ist das Reduzieren von Listen mittels der
reduce() Funktion. Hierbei wird eine Liste von links nach rechts abgearbeitet und zu einem Wert zusammengefasst. Das wohl wichtigste Beispiel für
reduce() ist die Fakultät:
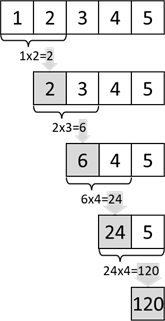
Abb.: 5: Berechnung Fakultät von 5
Die eigentliche Berechnung pro Elementepaar ist die Multiplikation – wir brauchen also für die auf die Liste angewendete Funktion zwei Parameter.
Listing 18: Funktionale Fakultätsberechnung
Kurze Erklärung der Codezeilen: Die Funktion
reduce() muss aus
functools importiert werden. Die eigentliche Funktionalität der Fakultätsberechnung ist durch Nutzung von
reduce() mit einer Zeile erledigt. Hierzu müssen wir mit
range() eine Liste erzeugen, welche die Zahlen 1 bis inklusive der Eingabezahl beinhaltet. Auf diese Liste wird nun mittels
reduce() eine (anonyme) Funktion mit zwei Parametern
x und
y angewendet. Diese gibt lediglich das Produkt
x * y zurück. Da
reduce() das Rechenergebnis nach dem Abschneiden des linken Feldes in das nun neue linke Feld schreibt, steht am Ende die Fakultät.
Führen wir den Code aus, erhalten wir die 120 als die Fakultät von 5. Natürlich lässt sich die Fakultät mit einer reinen Rekursion ohne Listen sehr viel einfacher lösen (siehe
Kapitel 9), aber für die Darstellung der Idee hinter
reduce() ist das Beispiel jedoch sinnvoll.

Rekursive Datentypen
Das letzte Thema, welches für den Einsteiger im Zusammenhang mit funktionaler Programmierung erwähnenswert ist, sind sogenannte „rekursive Datentypen“. Hierunter versteht man Datenstrukturen, welche wiederum eine
Referenz auf die gleichen Datenstrukturen haben und sich somit verketten lassen. Diese „verketteten Listen“ haben wir bereits in
Kapitel 7 kennengelernt. Eine weitere rekursive Datenstruktur ist ein Baum. Hier am Beispiel eines Stammbaums:
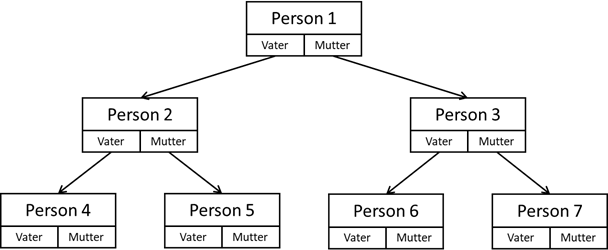
Abb.: 6: Baumstruktur
Der hier abgebildete Baum ist eine Sonderform von Baumstrukturen – ein binärer Baum, da jeder Knoten maximal zwei Kindknoten aufweist. Bevor wir uns nun ein einfaches Beispiel mit rekursiven
Datentypen ansehen, noch ein wichtiger Hinweis. Python ist von der Grundidee keine rein funktionale Programmiersprache. Aus diesem Grunde gibt es Arrays und Listen, welche mit Hilfe von
map(),
filter() und
reduce() sehr einfach verarbeitet werden können. Insofern ist die Nutzung von bspw. verketteten Listen erstmal nicht intuitiv. Die nun folgenden Beispiele sind also erstmal eher informativer Art.
Beginnen wir erstmal mit einem Code, welcher eine verkettete Liste erzeugt. Hierzu müssen wir nun (aufgrund der nicht ursprünglichen funktionalen Ausrichtung von Python sehr untypisch für funktionale Programmierung) in Python eine Klasse erzeugen, welche die Referenzierung auf das nächste Element
erlaubt. Hierzu benötigen wir lediglich eine Variable für einen Wert und eine für die Referenz auf das nächste Element:
Listing 19: Hilfsklasse für rekursive Datenstruktur
Als nächstes definieren wir eine Funktion, welche eine verkettete Liste einer vorgegebenen Länge erzeugt. Da wir bei funktionalen Programmiersprachen auf Schleifen verzichten, setzen wir diese Funktionalität traditionsgemäß als Rekursion um:
Listing 20: Erzeugung einer verketteten Liste beliebiger Länge
Kurze Erklärung der Codezeilen: Die Funktion muss in der Lage sein, die Verkettung umzusetzen. Da wir rekursiv arbeiten, benötigen wir hierfür eine Referenz auf das darunterliegenden Kind-Element als Parameter.
Beim initialen Aufruf können wir jedoch kein Element übergeben – wir wollen die Liste ja neu erzeugen. Also belegen wir den Parameter
childElmt auf das Kindelement initial mit
None. Der andere Parameter
numbElmt gibt an wie viele Elemente (noch) zu erzeugen sind. Zuerst kümmern wir uns innerhalb der Funktion erstmal darum, dass die Rekursion auch wirklich abbricht – indem die Anzahl der (noch) zu
erzeugenden Elemente auf 0 geprüft wird. Nur wenn
numbElmt größer 0 ist, müssen wir noch neue Elemente erzeugen. Dies erfolgt mit dem Konstruktoraufruf
Elmt(). Dieses Element erhält nun das übergebene Element als Kindelement – wir haben also mit dem Konstruktoraufruf das Elternelement des übergebenen Kindelementes geschaffen. Wenn in
childElmt None steht, so haben wir ein Elternelement ohne Kindelement geschaffen, was somit zum letzten Element der Kette wird. Nun rufen wir
createList() rekursiv auf, indem wir
numbElmt um eins reduzieren und das gerade erzeugte Element als Parameter übergeben. Dadurch wird es zum Kindelement des nächsten Elternelements. Sollte in der rekursiven Verarbeitung bei der Prüfung auf
numbElmt == 0 true herauskommen, so muss kein neues Elternelement erzeugt werden und das übergebene
childElmt wird zurückgegeben.
Bei einem Aufruf
createList(3) würde die Aufrufstruktur also wie folgt aussehen:
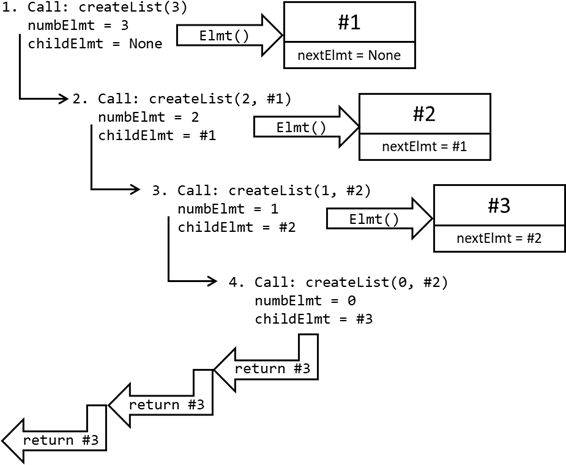
Abb.: 7: Rekursive Aufrufstruktur
Zuerst wird das letzte Element erzeugt und als Kindelement für die Erzeugung des vorletzten Elementes übergeben. Dieses wird wiederum als Kindelement des ersten Elementes übergeben. Die verkettete Liste hat somit drei Elemente:

Abb.: 8: Verkettete Liste mit drei Elementen
Das vorderste Element #3 wäre dadurch das Root-Element, da wir hierüber den Zugriff auf alle Elemente ermöglichen. Nun benötigen wir noch eine Funktion, welche bei einem Element auf einer vorgegebenen Position in der
Liste einen Wert setzt. Auch hier gehen wir den steinigen rekursiven Weg:
Listing 21: Rekursive Funktion zum Setzen von Werten in verketteter Liste
Kurze Erklärung der Codezeilen: Die Funktion
setElementVal() benötigt nun den zu setzen Wert
val, die Position
pos an der
val gesetzt werden muss und die Referenz auf ein Element, welches beim initialen Aufruf mit dem Root-Element belegt werden muss (in unserem Beispiel das Element #3). Nun prüfen wir, ob die Positionsangabe 0 ist
und wir an der aktuellen Stelle den Wert setzen dürfen. Wenn nicht, dann prüfen wir sicherheitshalber, ob überhaupt ein Kindelement vorhanden ist und rufen die Funktion rekursiv nochmal auf,
diesmal aber wird
pos um eins reduziert. Somit erfolgt die darüberliegende Prüfung nochmal.
Somit können wir nun eine Liste erzeugen und mit Werten belegen:
Listing 22: Erzeugung einer verketteten Liste mit den Werten 2, 4 und 6
Soweit ist das nun alles andere als trivial. Wenn wir uns überlegen, wie einfach wir diese Funktionalität mit einem Array erreichen würden, ist es schon fast merkwürdig, warum man solche Strukturen überhaupt umsetzt.
Aber sehen wir uns nun eine Funktion an, welche alle Elemente dieser Liste ausgibt:
Listing 23: Ausgabe aller Elemente einer verketteten Liste
Kurze Erklärung der Codezeilen: Die Funktion
printAllValues() erhält nun beim initialen Aufruf das Root-Element. Nun wird geprüft, ob das übergebene Element wirklich existiert. Wenn ja, dann geben wir den Wert aus. Im Anschluss daran rufen wir die Funktion mit dem nächsten
Elementes wieder auf. Wenn das aktuelle Element das letzte der Kette war, würde
None übergeben werden und in der nächsten Rekursion würde der Aufruf beendet werden.
Wenn wir also
printAllValues(root) aufrufen würden, sehen wir die Werte 2, 4 und 6 auf der Konsole. Wir sehen also, dass diese rekursiven Datentypen uns beim Thema „rekursive Funktionen“ sehr
entgegenkommen. So aufwändig die Erzeugung war, so einfach ist dann am Ende der Umgang mit diesen Konstrukten. Und wenn man genau hinsieht erkennt man, dass es für diese gesamte
Funktionalität lediglich eine einzige Stelle gibt, an der wir eine echte Zuweisung haben – und zwar bei der Belegung unserer Objektwerte, welche wir ja mangels einer „echten“ funktionalen Programmiersprache über die Klasse
Elmt modellieren mussten.
Weiter werde ich die Türe zur funktionalen Programmierung nun nicht aufstoßen – da es meines Erachtens für einen Programmieranfänger doch zu weit gehen würde. Trotzdem gehe ich davon aus, dass die Grundidee dieses
Programmierparadigmas erkannt wurde und man zumindest ansatzweise ein paar Ankerpunkte für weitere Schritte in diese Richtung mitnehmen kann. Was nachvollziehbar sein sollte ist, dass das eigentliche Ziel der
Klarheit im Code durch die funktionale Programmierung nur dann erreicht werden kann, wenn der Leser des Codes sich eingehend und intensiv mit den Konzepten beschäftigt. Ein Kapitel mit gerade mal elf Seiten kann
dies mit Sicherheit nicht leisten.
Was man aber mitnehmen sollte ist, dass die funktionalen Programmieransätze Funktionen hervorbringen, welche absolut gekapselt sind. Jede Funktion kann für sich sehr einfach getestet werden, da ausschließlich die Parameter
das Funktionsergebnis bestimmen. Das Fehlen von Seiteneffekten führt eben dazu, dass wir bei der Definition von Testdaten uns lediglich auf die Parameter der einzelnen Funktion konzentrieren müssen und nicht um irgendwelche
Variablen, welche außerhalb der Funktionen liegen.

CC Lizenz (BY NC SA)
