Von Nullen und Einsen
Bevor wir uns um die einzelnen Programmiersprachenelemente kümmern, müssen wir uns mal ansehen, was ein Rechner
überhaupt macht. Wie funktioniert er im inneren seines Kerns? Es ist klar, dass wir uns hier nicht mit den feinsten
Details einer CPU (Central Processing Unit) eines Rechners auseinandersetzen können – ein paar elementare Ideen,
die sich seit der Erfindung des Computers in den 40er Jahren aber nicht wirklich grundlegend geändert haben,
sollten wir aber durchaus beleuchten.
Die allerersten technischen Rechenmaschinen hatten – neben der fehlenden Programmierbarkeit – einen entscheidenden
Nachteil in ihrer Konstruktion. Sie nutzten das Dezimalsystem als Basis in der Verarbeitung. Erst als man sich auf das
Binärsystem konzentrierte, konnten die einzelnen Funktionalitäten sehr viel flexibler realisiert werden. Der Vorteil
des Binärsystems war, dass die technische Umsetzung von nur zwei Zuständen, nämlich 0 und 1 in Form von „keine
elektrische Spannung angelegt“ und „elektrische Spannung angelegt“, sehr einfach und zuverlässig möglich ist.
Hinzu kommt, dass sich die Komplexität der Verarbeitung im Rahmen der Booleschen Logik(1) in Grenzen hielt. Für uns
als Programmierer ist die Historie zwar nicht wirklich wichtig, die Gründe der damaligen Lösungen und somit die
dahinterliegenden Grundsätze sollten wir aber auf jeden Fall verstehen, da sie immer noch gültig sind.
(1) George Boole, englischer Mathematiker und Logiker

Logikgatter
Beginnen wir mit den logischen Zusammenhängen, die von George Boole formal festgehalten wurden. Die Grundidee ist,
dass es nur zwei Zustände gibt – meist 1 und 0 oder „wahr“ und „falsch“ bzw. englisch „true“ und „false“ genannt.
Diese Zustände können nun logisch verknüpft werden. Ein Beispiel von außerhalb der Computerwelt: Wir wollen ein
Spiegelei braten. Zuerst prüfen wir, ob im Kühlschrank ein Ei finden. Danach sehen wir nach, ob im Schrank eine
Pfanne ist. Dann können wir loslegen. Die erste Bedingung wäre also „Ei im Kühlschrank vorhanden“ => „wahr“. Die
zweite Bedingung ist „Pfanne in Schrank vorhanden“ => „wahr“. Wenn also die erste Bedingung und die zweite Bedingung
erfüllt ist, können wir das Ei braten. Damit haben wir schon die erste Regel, die UND Verknüpfung formuliert:
Ergebnis ist „wahr“, wenn Bedingung 1 UND Bedingung 2 erfüllt sind.
Im Umkehrschluss heißt dies aber auch, dass das Ergebnis „falsch“ ist, wenn mindestens eine der beiden Bedingungen
eben auch „falsch“ ist. Um das etwas griffiger darzustellen, gibt es jetzt mehrere Möglichkeiten. Eine wäre mit
Hilfe von schriftlichen Symbolen:
X = A ∧ B
Diese Notation eignet sich hervorragend für die Anwendung der Booleschen Algebra, mit deren Hilfe man komplizierte
Ausdrücke analysieren und vereinfachen kann. Für Programmierer wird dies aber eher selten benötigt. Eine weitere –
auch für Programmierer eher selten genutzte – Möglichkeit ist die Nutzung von Schaltsymbolen. Hier werden die
einzelnen Verknüpfungen mit genormten Symbolen dargestellt. Das Ziel dieser Symbole ist im Regelfall das Design
von tatsächlichen Schaltungen, weshalb man die Verknüpfungen oft auch „Gatter“ nennt. Unsere UND Verknüpfung würde
hiernach wie folgt aussehen:

Abb.: 1: UND Gatter Symbol
Der für uns als Programmierer wahrscheinlich sinnvollste Ansatz für den Umgang mit Logikverknüpfungen ist jedoch die
Wertetabelle. Hier werden alle Eingangskombinationen und die jeweils hierfür gültigen Ausgangswerte tabellarisch
dargestellt:
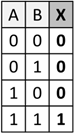
Abb.: 2: UND Verknüpfung Wertetabelle
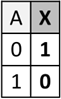
Die „1“ steht hier für „wahr“ und die 0 entsprechend für „falsch“. Durch diese „Wertetabelle“ können wir das Verhalten
am besten verstehen und müssen auch nicht lange Erklärungen für die einzelnen unterschiedlichen Funktionen anfertigen.
Sehen wir uns mal die wichtigsten Verknüpfungen an. Da es bei zwei Eingängen oftmals Interpretationsprobleme bei
Sonderfällen gibt, stelle ich sie bei den Verknüpfungen gleich mit drei Eingängen dar:
| Name: | UND | ODER | Exlusiv ODER | Negation |
|---|---|---|---|---|
| Wertetabelle: | 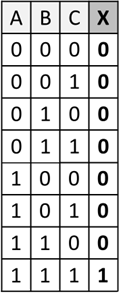 |
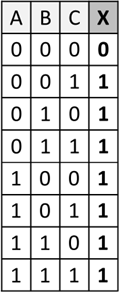 |
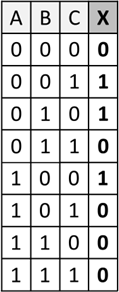 |
 |
| Schaltsymbol: |  |
 |
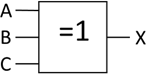 |
 |
| Schriftzeichen: | X = A ∧ B ∧ C | X = A ∨ B ∨ C | X = A ⊻ B ⊻ C | X = A |
| Funktionsbe- schreibung: |
X ist 1, wenn alle Eingänge 1 sind. | X ist 1, wenn min-destens ein Eingang 1 ist. | X ist 1, wenn exakt ein Eingang 1 ist. | X ist das Gegenteil von A. |
Tabelle 1: Elementare Logikgatter
Basierend auf diesen Logikbausteinen kann man theoretisch einen Computer bauen. Natürlich ist die Welt wie immer
komplizierter als die Theorie, aber für das Programmierverständnis reicht diese Einschätzung aus. Was bei den
Tabellen vielleicht auffällt ist, dass die Nullen und Einsen der Eingänge A, B und C in einem bestimmten Muster
angeordnet sind. Das muss zwar so nicht sein, hilft aber dabei, keine Kombination zu vergessen. Dieses Muster ist
nicht zufällig gewählt, sondern folgt den Regeln eines positionellen Zahlensystems, so wie unser Dezimalsystem – nur
eben mit weniger Ziffern. Um das nun zu verstehen, gehe ich nochmal kurz auf die Konzeption unseres Dezimalsystems
ein und übertrage es auf das vom Computer genutzte Binärsystem.
Binärzahlen
Wie vermutlich noch die meisten aus der Schule wissen, ist unser Zahlensystem streng logisch aufgebaut. Wir haben
einen Zeichenvorrat von 10 Ziffern (weshalb man auch von der „Basis 10“ spricht), die basierend auf ihrer Position
in der dargestellten Zahl eine bestimmte Wertigkeit besitzen. Wenn wir die Zahl 385 nehmen, dann können wir die
Zahl auch wie folgt sehen:
385 = 3 x 100 + 8 x 10 + 8 x 1
Man kann die Zahlen für die Wertigkeit (100, 10 und 1) auch systematischer darstellen, indem man sie in Relation mit
der Basis bringt:
385 = 3 x 102 + 8 x 101 + 8 x 100
Das Schöne daran ist nun, dass wir mit diesem Konzept einfach die Basis austauschen können und es funktioniert immer
noch. Bei der booleschen Logik haben wir gesehen, dass wir „nur“ zwei Zustände haben. Insofern liegt es nahe, dass wir
hier ein Zahlensystem benötigen, welches auch nur zwei Ziffern besitzt – nämlich die 0 und die 1. Jetzt können wir die
Zahlen sowohl im Dezimalsystem als auch im Binärsystem (man sagt auch Dualsystem) gegenüberstellen:
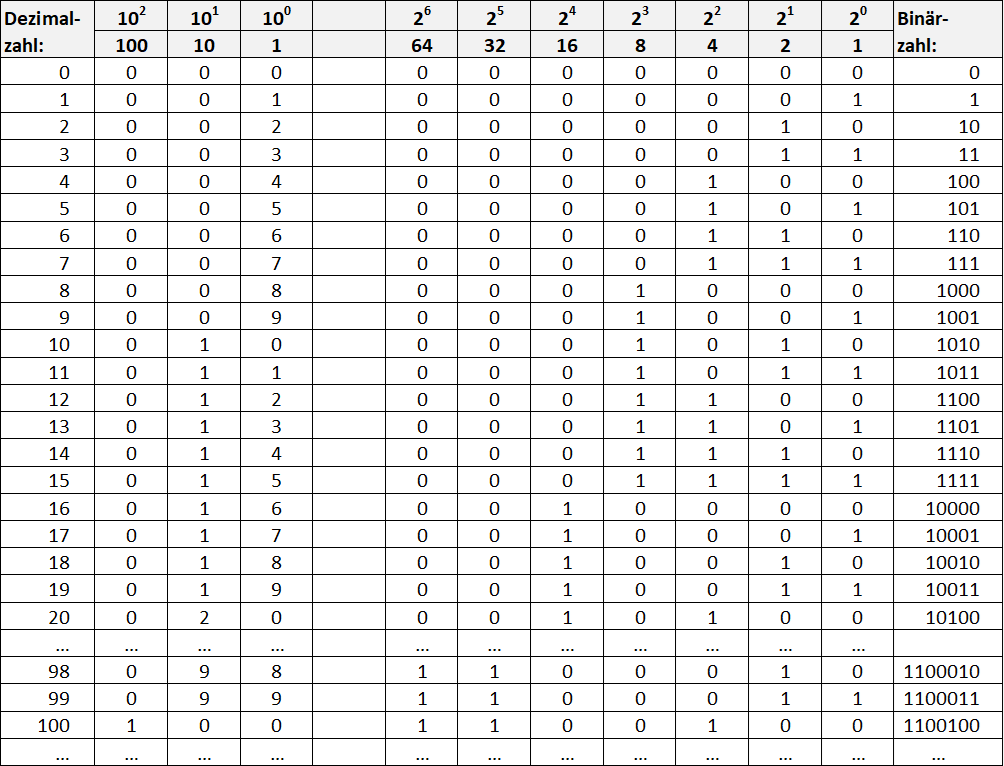
Tabelle 2: Gegenüberstellung Dezimal vs. Binärzahlen
Zuerst einmal fällt auf, dass uns die Werte der einzelnen Stellen des Binärsystems sehr vertraut vorkommen. Die
Zahlenwerte der Zweierpotenzen finden wir in vielen Speicherangaben von digitalen Geräten wieder – „das Handy hat
einen Speicher von 64 Gigabyte“. Dies liegt schlichtweg daran, dass die Speicher in digitalen Geräten eben mit
Adressen basierend auf dem Binärsystem verwaltet werden. Weiterhin fällt auf, dass wir ohne die Angabe, um welches
Zahlensystem es sich handelt, die Zahl 100 beispielsweise nicht interpretieren können. Um dies in den Griff zu
bekommen, schreibt man in Situationen, in denen das Zahlensystem nicht klar ist, die Basis als tiefergestellte Zahl
hinzu. Bspw. ist 1002 die „eins null null“ im Binärsystem, was Dezimal die 4 währe –
korrekterweise 410. In Computerprogrammen können wir im Code aber keine Zahlen
„tiefstellen“, weshalb es dort eine andere Notation gibt. Die Zahl 1002 würde im Code
in den meisten Programmiersprachen mit 0b100 hinterlegt werden, wir stellen also den Präfix „0b“ davor, der „Binär“
markiert. Dezimalzahlen benötigen im Code diesen Präfix jedoch nicht, da Dezimal der Standard ist. Insofern
vereinbaren wir auch für dieses Buch, dass wir ab jetzt alle Zahlen ohne gesonderte Markierung immer im Dezimalsystem
interpretieren, es sei denn das Zahlensystem geht eindeutig aus dem Kontext hervor.
Wir können nun jede beliebige ganze positive Zahl(2) als Binärcode darstellen. Die
Frage ist nun, was könnten wir mit diesen Zahlen anstellen? Erstmal ist es möglich, mit Hilfe von Logikverknüpfungen
„bitweise“ vorzugehen. Dies bedeutet, dass wir zwei Binärzahlen Stelle für Stelle (der Informatiker spricht hier
von „Bit für Bit“) mit einem logischen Operator verknüpfen. Probieren wir mal die beiden Zahlen 10012
und 112 (also 910 bzw. 310) mit
Hilfe einer ODER Verknüpfung zu verarbeiten. Hierzu schreiben wir die beiden Zahlen im Binärformat untereinander und
wenden die ODER Regel Bit für Bit an:
(2) Über die negativen und Gleitkommazahlen werden wir später nochmal sprechen müssen.
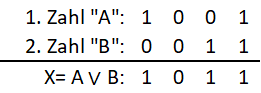
Abb.: 3: ODER Funktion
Beginnend rechts ermitteln wir „1 ODER 1 ergibt 1“. Bei der nächsten Stelle gilt „0 ODER 1 ergibt 1“. Dann „0 ODER 0
ergibt 0“ und schließlich „1 ODER 0 ergibt 1“. Somit ist das Ergebnis 1011(also 92 bzw.
11(also 910 im Dezimalsystem. Die Frage ist nun – was bringt uns das? Zum einen die
Erkenntnis, dass wir Zahlen, egal in welchem Zahlensystem sie angegeben sind, immer auch als Binärzahl darstellen
können, womit wir die Aussage „9 ODER 3 ergibt 11“ programmieren können. Wir werden später sehen, dass wir dieses
Konzept beim Programmieren tatsächlich sinnvoll einsetzen können(3). Der eigentliche
Sinn dieser Operationen ist allerdings viel weitreichender.
(3) Dies wird bei Übergabeparameter von mehreren Flags sich als praktisch erweisen

Addierer
Eine für alle wohl sinnvolle Operation mit zwei Zahlen ist die Addition. Nun können wir unsere beiden Zahlen 9
und 3 sehr einfach im Kopf addieren und erhalten die 12. Wir hätten aber gerne, dass diese Addition über ein
technisches Gerät realisiert wird. Hierzu müssen wir uns die Idee des Addierens nochmal in seine Einzelteile zerlegen
– und das machen wir am besten in dem uns bekanntesten Zahlensystem, dem Dezimalsystem. Konzentrieren wir uns
hierbei nur auf zwei einstellige Zahlen. Die Möglichkeiten sind hier schon mal sehr hoch, nämlich 10 x 10, sprich
100 Kombinationen – wir müssen 0 + 0 wissen, dann 0 + 1, 0 + 2 usw. bis 9 + 9:

Abb.: 4: Alle möglichen einstelligen Additionen im Dezimalsystem
Dies technisch umzusetzen wäre schon mal recht aufwändig. Jetzt kommt aber unsere Erkenntnis, dass wir auch das Binärsystem
verwenden können, sehr entgegen. Hier haben wir nur zwei Ziffern, insofern reduziert sich der Möglichkeitsraum auf
2 x 2 = 4:
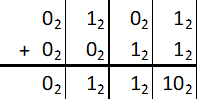
Abb.: 5: Alle möglichen einstelligen Additionen im Binärsystem
Dies können wir nun als Wertetabelle formulieren. Da wir zwei Einstellige Zahlen addieren, gibt es zwei Eingänge. Als
Ergebnis erhalten wir eine zweistellige Zahl, was wiederum zwei Ausgänge erfordert:
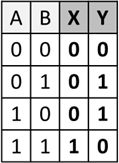 bzw. als einzelne Wertetabellen:
bzw. als einzelne Wertetabellen:
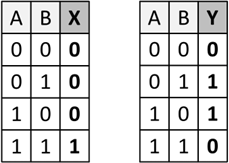
Abb.: 6: Binäre Addition als XOR und UND
Wir können das Ganze aber auch anders formulieren:
X = A ∧ B und Y = A ⊻ B
Dies bedeutet, dass wir nun in der Lage sind ein Schaltbild für die Addition von zwei einstelligen Binärzahlen zu
entwerfen, das man auch „Halbaddierer“ nennt:
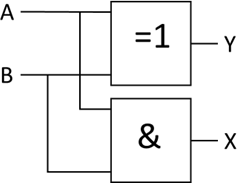
Abb.: 7: Halbaddierer
Die beiden Ausgänge würde man in der Schaltungstechnik anders benennen – Y wäre die Summe „s“ und X der Übertrag
(englisch „carry“) „c“. Mit weiteren logischen Gattern kann man nun aus mehreren Halbaddierern einen Volladdierer
bauen, der nun auch mehrstellige Binärzahlen verarbeiten kann. Ich verzichte hier auf die detaillierte Darstellung
eines Volladdierers, da es uns hier nur um das Grundverständnis geht. Die Quintessenz für uns Programmierer aus
diesen Überlegungen allerdings ist, dass das Addieren von Zahlen eine der grundlegendsten Eigenschaften von Computern
ist, welche auf dem Prozessor als logische Schaltung verbaut ist. Wenn wir uns im Gegensatz dazu die Multiplikation
ansehen, muss hier schon mehr gemacht werden. Ein – zugegebenermaßen naiver – Ansatz wäre, eine Multiplikation aus
mehreren Additionen aufzubauen. Beispielsweise kann 3 * 5 auch als 5 + 5 + 5 gerechnet werden. Wenn man eine Zeitmessung
von solchen Operationen macht, stellt man aber fest, dass die Multiplikation nicht um ein Vielfaches langsamer ist als
die Addition. Die Compiler und auch die Chiphersteller haben da noch einige „Tricks“ auf Lager. Auch hier werde ich
die Türe einen kleinen Spalt aufstoßen, damit wir eine Idee davon haben, dass die „naiven“ Ansätze nicht immer die
einzigen sind.

Multiplizierer
Gehen wir hierzu mal wieder auf unser binäres Zahlensystem. Nehmen beispielsweise mal die Zahl 1011012,
was im Dezimalsystem die Zahl 45 wäre. Und nun fügen wir am rechten Ende einfach eine 0 hinzu. Dadurch erhalten wir die
Zahl 10110102. In Dezimal haben wir damit die 90 erhalten. Dies entspricht eine Multiplikation
mit 2. Dies ist insofern logisch, als dass wir beim Hinzufügen einer 0 im Dezimalsystem im Prinzip auch „nur“ mit 10
multiplizieren. Wenn ich bspw. bei der Zahl 14 eine 0 rechts hinzufüge, ist dies nichts anderes als 14 * 10 = 140.
Da im Binärsystem die Basis 2 ist, bedeutet die „Verschiebung“ der Ziffern um eine Stelle nach links eine Multiplikation
mit 2, die Verschiebung um 2 Stellen die Multiplikation mit 4, um 3 Stellen mit 8 usw. Somit können wir bspw. eine
Multiplikation mit 9 x 5 wie folgt aufbauen:
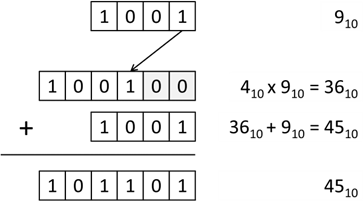
Abb.: 8: Binäre Multiplikation mit Bitshift und Addition
Wir schieben die 9 um zwei Bit nach links, was einer Multiplikation mit 4 gleichkommt. Danach addieren wir nochmal die
9 hinzu und haben somit die Rechnung 9 x 9 = 4 x 9 + 9, was entsprechend die 45 ergibt.
Dies ist somit eine simple Reduktion der Operationen – zumal das Verschieben der Bits (somit auch „Bitshift“ genannt)
mit eine der einfachsten Operationen überhaupt ist. Das Ziel, welches die Hersteller von Computersystemen damit
verfolgen ist ganz einfach die Erhöhung der Rechengeschwindigkeit. Wenn wir nun eine Art Hierarchie der Operationen
aufstellen, dann ist wohl Addition die einfachste, gefolgt von Subtraktion, Multiplikation und am Ende die Division –
wobei wir hier die Restoperation(4) und die Division getrennt voneinander betrachten müssten.
Wenn wir also bei der Implementierung von Algorithmen sehr auf die Ausführungsgeschwindigkeit achten müssen, so kann die
ein oder andere Designentscheidung auch davon abhängen, welche Operationen wir verwenden müssen. Hierzu werden wir uns
später nochmal im Rahmen der Primzahlberechnung ein praktisches Beispiel ansehen.
(4) Die Operationen werden später noch genauer betrachtet – so viel vorab: Restoparation ist der Rest der ganzzahligen Division.

Hexadezimalzahlen
Vielleicht hat der ein- oder andere neben den beiden Zahlensystemen „Dezimal“ und „Binär“ auch schon den Begriff
„Hexadezimal“ gehört. Gerade in der Programmierung kommt uns dieses Zahlensystem öfter in die Quere. Der einzige
Sinn des Hexadezimalsystems ist es, eine kompaktere Schreibweise von Binärzahlen zu ermöglichen. Man kann sich das
Hexadezimalsystem wie eine Komprimierung von Binärzahlen vorstellen. Wie der Name schon sagt, ist die Basis „Hexadezimal“
die 16, wodurch wir eine Hexadezimalzahl auch entsprechend notieren, bspw. 14216 (bzw.
wäre es in Computerprogrammen 0x142). Damit haben wir einen Zeichenvorrat von 16 Zeichen für unsere Zahlendarstellung.
Der Einfachheit halber hat man die Ziffern 0 bis 9 und dann die Buchstaben a bis f definiert (wobei hier die Groß- bzw.
Kleinschreibung keine Rolle spielt). Das Konzept ist nun genauso wie bei den anderen Zahlensystemen. Wir können unsere
Tabelle der beiden Zahlensysteme nun um die Hexadezimalwerte ergänzen:
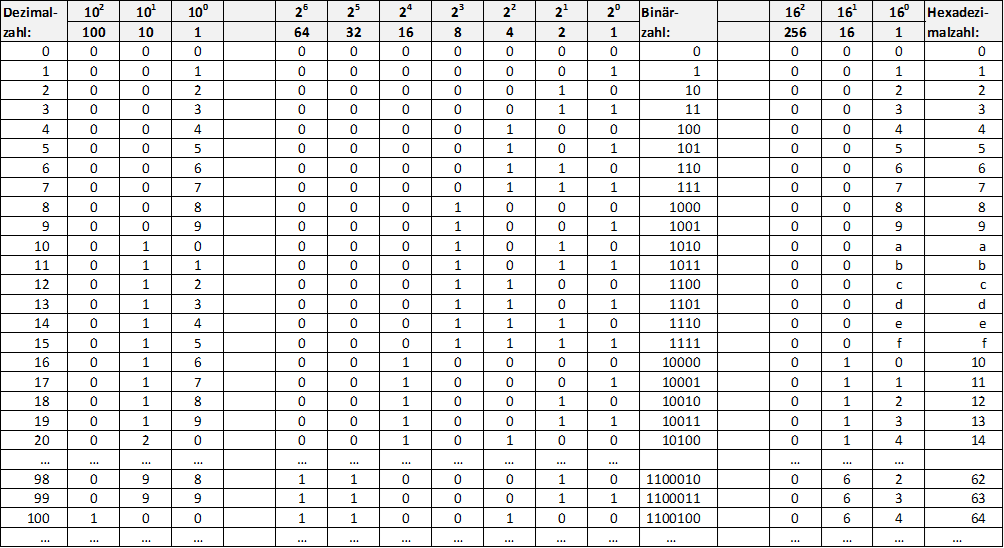
Abb.: 9: Gegenüberstellung Dezimal vs. Binär vs. Hexadezimalzahlen
Der entscheidende Punkt ist, dass die Basis 16 auch eine Zweierpotenz ist, nämlich 2 hoch vier. Dadurch können wir
jeweils Vierercluster von Bits definieren, welche einer Hexadezimalziffer entsprechen. Da der Computer intern Binärzahlen
verarbeitet und wir an vielen Stellen Informationen für den Computer bereitstellen wollen, können wir hiermit in einer
verkürzten Form diese Daten angeben. Dies wird unter anderem bei Farbangaben in Webseiten benötigt. Wenn wir beispielsweise folgende
Binärzahl haben: 1110100110010110011110102 (was übrigens der HTML Farbcode „dark salmon“ ist),
dann können wir uns vorstellen, wie unhandlich der Umgang mit diesem „Ungetüm“ ist. Wir könnten nun den Wert in Dezimal
umrechnen, was per Hand sehr aufwändig ist. Mit dem Taschenrechner würde hier die 15.308.410 herauskommen. Die Umrechnung
in Hexadezimal kann man jedoch aufgrund dieser Vierercluster problemlos im Kopf machen – sofern man für die Hexadezimalziffern
0 bis f die Binärzahlen weiß. In unserer Tabelle 3 wären dies die ersten 16 Zeilen. Der Weg ist nun, dass wir von rechts
beginnend unsere Binärzahl in Vierergruppen aufteilen und zu jeder Vierergruppe die zugehörige Hexadezimalziffer notieren:

Abb.: 10: Umwandlung von Binär- in Hexadezimalzahlen
Wenn man nun im Netz mal nach der „html farbe dark salmon“ sucht, wird man ziemlich schnell auf irgendwelche Webseiten
stoßen, die den Hexadezimal Code (oder Kurz Hexcode) „0xe9967a“ anzeigen. Es ist also sehr gebräuchlich, bei der
Computertechnik mit Hexadezimalwerten zu arbeiten.

CC Lizenz (BY NC SA)
