Performance – wenn’s schnell gehen muss
Wenn man bis hierher alles so weit verstanden hat und in der Lage ist es anzuwenden, ist man bereits einen Riesenschritt in Richtung Programmierer gegangen. Man hat alle Werkzeuge in der Hand,
Algorithmen umzusetzen. Der nächste logische Schritt ist es, diese Algorithmen auch effizient zu gestalten, so dass sie möglichst wenig Ressourcen benötigen. Hier finden wir im Wesentlichen zwei
relevante Größen, Zeit (was eigentlich CPU-Leistung ist) und Speicher. Leider schließen sich diese beiden Größen manchmal aus. Die Beschleunigung eines Algorithmus erkauft man sich mitunter mit
einem erhöhten Speicherbedarf. Wir werden solch einen Fall später in diesem Kapitel sehen. Aber auch das tiefere Verständnis von Zusammenhängen innerhalb einer Programmiersprache hilft oftmals,
die Algorithmen schneller zu gestalten.

Insight Knowledge
Ein Beispiel wäre hier das Wissen darüber, ob ein Objekt immutable ist – sprich ob es nach der Erzeugung nicht mehr geändert werden kann. In Java wäre dies das Stringobjekt. Sehen wir uns hierfür folgenden Code an:
Listing 1: Stringanpassung als Performancebeispiel in Java
Kurze Erklärung der Codezeilen: Das Programm macht eigentlich nichts wirklich Sinnvolles, es soll lediglich das Stringverhalten transparent machen. Wir erzeugen einen leeren
String. Danach holen wir uns einen Zeitstempel und speichern diesen für eine spätere Zeitmessung ab. Nun laufen wir eine Schleife 100.000 mal durch und hängen jedesmal ein
"X" hinten an. Danach ermitteln wir wieder die Zeit und bilden die Differenz, wodurch wir die Durchlaufzeit unseres Algorithmus haben.
Wenn wir dieses Programm laufen lassen, erhalten wir also die Durchlaufzeit, welche je nach Rechner natürlich unterschiedlich sein kann. Auf meinem System erhalte ich 679 Millisekunden. Nun wissen wir ja,
dass Java Strings immutable sind, weshalb bei jedem Durchlauf ein neuer String erzeugt werden muss, der eine Kopie des Vorgängers plus einem „X“ ist. Früher oder später muss dann auch noch der
Garbage Collector die vielen „alten“ Strings aufsammeln und freigeben. All das kosten Zeit. Um nun solch einen Algorithmus schneller zu machen, benötigen wir etwas, das eben nicht immutable ist und somit dieser
Overhead wegfällt. In Java wäre dies der
StringBuffer. Schreiben wir also unseren Code um:
Listing 2: Performantere Lösung mit Stringbuffer
Kurze Erklärung der Codezeilen: Der sukzessive Aufbau des Strings wird nun mit einem
StringBuffer mit
append() durchgeführt. Erst wenn dieser fertiggestellt wurde, übergeben wir den
String als Ganzes in die Variable
myOut.
Die Verarbeitungszeit dieses Programms hat sich nun auf ganze 4 Millisekunden verkürzt! Unser erstes Programm hat sich also mehr um Overhead als um den eigentlichen Algorithmus gekümmert.
Solche Optimierungen können wir jedoch nur vornehmen, wenn wir die internen Abläufe verstehen – was mitunter eine echte Herausforderung darstellt.

Architektur
Ein weiterer Punkt, den man bei sehr performancekritischen Applikationen in Betracht ziehen muss, ist die verwendete Architektur. Hierfür bauen wir uns ein Programm, welches alle Primzahlen(1) von 2 bis zu einer Obergrenze ermittelt und in einem Array hinterlegt. Für den ersten Schritt setzen wir diesen Algo-rithmus relativ „naiv“ um, indem wir einfach nur blind alle kleineren Zahlen auf Teilbarkeit prüfen:
(1) Primzahl: Zahl, welche lediglich 1 und sich selbst als ganzzahligen Teiler besitzt, also Zahl%Teiler ungleich 0 für alle Teiler ungleich 1 und Zahl
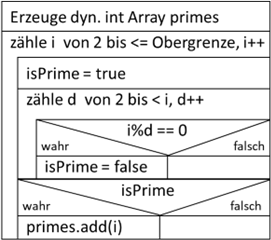
Abb.: 1: Primitives Suchen nach Primzahlen
Wir erzeugen ein dynamisches Array, wo wir die gefundenen Primzahlen ablegen. Danach laufen wir alle Zahlen von 2 (als kleinstmögliche Primzahl) bis zur gesuchten Obergrenze durch, indem wir die Zählvariable
i durchiterieren. Initial gehen wir erstmal davon aus, dass die aktuelle Zahl
i eine Primzahl ist, weshalb wir das Flag
isPrime auf
true setzen. Nun suchen wir einen Teiler
d in der zweiten Schleife. Hierzu laufen wir wieder von 2 bis kleiner der zu prüfenden Zahl
i durch. Wenn wir einen ganzzahligen Teiler finden, wird die Modulooperation = 0 (also Division ohne Rest) ergeben. Wenn dieser Fall mindestens einmal eintritt, dann war die Annahme,
i sei eine Primzahl falsch und wir setzen
isPrime auf
false. Nachdem wir alle möglichen (und unmöglichen) Teiler geprüft haben können wir anhand
isPrime feststellen, ob wir mindestens einen Teiler gefunden haben und
i entweder in die Primzahlenliste mit aufnehmen oder eben nicht. Dieser Algorithmus ist nun alles andere als performant! Wir werden ihn gleich noch optimieren – aber für’s Erste liefert er
erstmal zuverlässig alle Primzahlen bis zur Obergrenze.
Wenn ich diesen Algorithmus nun in Java umsetze, dann sieht der Code wie folgt aus:
Listing 3: Primitiver Primzahlenalgorithmus in Java
Wenn ich diesen Code mit einem
maxVal Wert von 100.000 auf meinem Rechner laufen lasse, erhalte ich eine Durchlaufzeit von ca. 9 Sekunden (8421 Millisekunden). Den gleichen Algorithmus lasse ich nun mit allen
anderen hier besprochenen Programmiersprachen laufen und trage die Zeiten an. Diese sind nur Indikatoren – es handelt sich nur um einmalige Snapshots und nicht um Messreihen über mehrere Stunden.
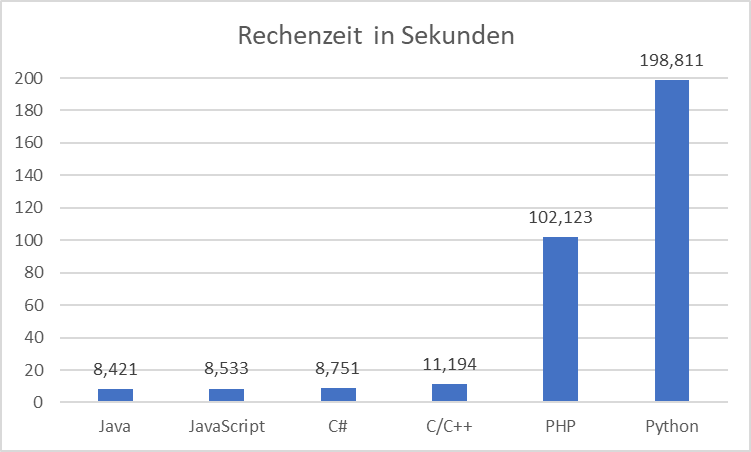
Abb.: 2: Rechenzeit verschiedener Architekturen
Python schneidet hier überraschend schlecht ab. Durch die Nutzung von Arrays statt Listen kann die Performance noch etwas verbessert werden, aber unterm Strich sehen wir eine deutliche Überlegenheit der
kompilierten Programmiersprachen und interessanterweise auch JavaScript. Gerade JavaScript sticht hier unter den Skriptsprachen heraus. Das ist deshalb bemerkenswert, weil JavaScript und Python vom Ansatz her
ähnlich sind – beide sind interpretiert, singlethreaded und typisieren dynamisch. Weiterhin sind sie in der ersten Hälfte der 90er Jahre entstanden. Es ist allerdings zu vermuten, dass aufgrund des Einsatzes
in Webbrowsern ein größeres wirtschaftliches Interesse an JavaScript vorherrschte, was eine entsprechende höhere Bereitschaft erklären würde, Entwicklungsbudget in JavaScript zu stecken – was zum JIT Compiler
geführt hat. Die logische Frage ist nun, warum ausgerechnet Python für Anwendungen im KI-Bereich sehr beliebt ist? Die Antwort liegt in der schnellen Erweiterbarkeit von Python durch externe C oder C++ Module.
Wenn ich also in Python einen wirklich schnellen Algorithmus benötige, schreibe ich hierfür eine C oder C++ Routine und binde sie in meinen Python Code ein(2).

17.3 Algorithmische Optimierung
Nun haben wir den Primzahlenalgorithmus in der schlechtesten aller denkbaren Algorithmen umgesetzt. Es werden unglaublich viele „unnütze“ Operationen durchgeführt, welche bereits im Vorfeld durch logische Überlegungen
eliminiert werden können. Versuchen wir nun also, den Algorithmus als solches Schritt für Schritt zu beschleunigen. Hierzu sehen wir uns nochmal das Struktogramm an. Die wohl einfachste Verbesserung ist, wenn wir die
innere Schleife abbrechen, sobald wir einen Teiler gefunden haben. Wenn wir bspw. bei der Zahl 15 festgestellt haben, dass sie durch 3 teilbar ist, müssen wir nicht auch noch nachweisen, dass 15 durch 5 teilbar ist.
Ein einziger ganzzahliger Teiler reicht um zu beweisen, dass 15 keine Primzahl ist. Bauen wir also in unseren Java Code ein break ein und lassen es wieder laufen:
Listing 4: Abbruch der inneren Schleife für ersten „Erfolgsfall“
Die Laufzeit in Java hat sich nun um ca. 90% von 8421 Millisekunden auf 828 Millisekunden reduziert. Dies ist schon mal eine enorme Verbesserung! Nun gibt es noch einen weiteren Verbesserungspunkt. Wir haben
die innere Schleife bis kleiner i, also der zu testenden Zahl laufen lassen. Dies ist insofern auch ineffizient, als dass wir wissen, dass der größtmögliche sinnvolle Teiler nicht größer als i/2 sein kann.
Wenn wir bspw. die 12 ansehen, dann ist 12/2 gleich die 6, da 2 x 6 gleich 12 ist – die beiden Faktoren sind also 2 und 6. Jede größere Zahl als 6 würde somit einen kleineren zweiten Faktor erfordern.
Dieser kann aber bei ganzzahligen Faktoren nicht kleiner als 2 sein, womit bspw. die 7 unmöglich ein ganzzahliger Teiler von 12 sein kann. Bauen wir auch dies in unseren Code ein, wobei wir hier darauf
achten müssen, dass wir das Istgleich nach dem < Zeichen nicht vergessen:
Listing 5: Begrenzung der inneren Schleife auf i/2
Nun liegen wir mit unserer Ausführungszeit nochmal 50% tiefer, bei 420 Millisekunden. Hier sei nochmal ein kurzer Hinweis zum Compiler erlaubt. Wenn wir uns die innere Zählschleife ansehen, finden wir hier den
Vergleich auf
i/2 was bedeutet, dass der Rechner eigentlich bei jedem Durchlauf der inneren Zählschleife
i/2 bilden muss – also jedes mal die gleiche Rechnung durchzuführen hat. Eigentlich wäre folgender Code besser:
Listing 6: Begrenzung der inneren Schleife auf i/2 ohne redundante Rechnungen
Wir merken uns die Obergrenze einmalig bei Start der Schleife in der Variablen
g mit dem Wert
i/2 und müssen somit anstatt in jedem Durchlauf, die Division durch 2 nur am Anfang – eben nur einmal durchführen. Die Rechenzeit mit diesem Code nimmt jedoch nicht ab! Diese Optimierung scheint also nichts
zu bringen. Dies liegt schlichtweg daran, dass der Compiler diesen Zusammenhang erkennt und selbstständig den Code so schreibt, dass keine unnötigen redundanten Berechnungen durchgeführt werden. Sehen wir
uns das Gleiche in PHP an, wo wir keinen Compiler involviert haben, reduziert sich die Durchlaufzeit mit und ohne der Variablen
g um weitere 25%. JIT Compiler würden dies übrigens auch optimieren, was eine Implementierung des Algorithmus in JavaScript zeigen würde.
Der nächste Optimierungsschritt geht noch tiefer in die Mathematik. Sehen wir uns mal die möglichen Teiler von 100 in einer Grafik an, in der wir die beiden ganzzahligen Faktoren a und b für a x b = 100 antragen:
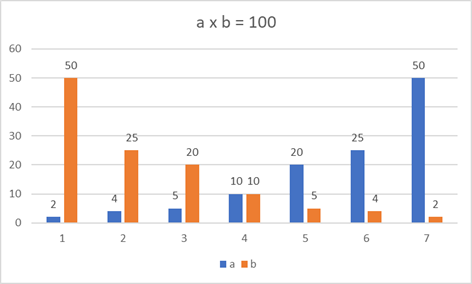
Abb.: 3: Faktoren von 100
Wir erkennen an dieser Stelle einen mathematisch offensichtlichen Zusammenhang. Der kleinste Wert von a (also 2) mutlipliziert mit dem größten Wert von b (für 100 ist dies 50) ist mathematisch die gleiche Rechnung wie der kleinste
Wert von b mutlipliziert mit dem größten Wert von a. Der Mathematiker kennt dies als das Kommutativgesetz der Multiplikation: „a mal b ist b mal a“. Das bedeutet, dass wenn wir den kleinsten Faktor von 100, also die 2 finden, haben
wir automatisch auch den größten, die 50 gefunden. Wir müssen also für eine vollständige Abdeckung der möglichen Multiplikationen nicht die Faktoren bis 50 prüfen, sondern es genügt bis zu dem Faktor a zu prüfen, der maximal genauso
groß ist wir Faktor b – sprich bis zu dem Punkt a2 = 100, was die Wurzel aus 100 = 10 ergibt. Dieser Punkt ist logischerweise genau in der Mitte unserer Grafik aus
Abbildung 3. Insofern können wir nun unseren Code noch weiter optimieren:
Listing 7: Begrenzung der inneren Schleife auf Wurzel von i ohne redundante Rechnungen
Die Ausführungszeit ist nun auf 20 Millisekunden geschrumpft, wobei diese Zahl um 100% schwankt, da wir teilweise unter der Messgenauigkeit unseres Timers liegen. Um nun sinnvolle Messwerte zu erhalten, müssen wir unsere Obergrenze von
100.000 auf 10.000.000 erhöhen und erhalten nun bei Java eine Rechenzeit von ca. 10.876 Millisekunden oder eben 11 Sekunden. Der nächste Optimierungsschritt geht noch weiter in die Mathematik hinein. Gehen wir mal davon aus, wir
möchten die Zahl 60 daraufhin prüfen, ob es sich um eine Primzahl oder um keine Primzahl handelt. Man könnte jetzt auf die Idee kommen zu sagen „60 ist 2 x 30, also keine Primzahl“. Die Faktoren 2 und 30 stecken tatsächlich in 60.
Nun sehen wir uns aber die 2 und 30 etwas genauer an. 2 ist im Gegensatz zu 30 bekanntlich selbst eine Primzahl. Wenn 30 aber keine Primzahl ist, dann müssen wir für die 30 wieder zwei Faktoren finden, welche die 30 bilden – hierfür
nehmen wir die 2 und 15. Hier gilt das Gleiche wieder, 2 ist eine Primzahl, 15 nicht. 15 können wir wieder zerlegen in 3 und 5, was nun schlussendlich beides Primzahlen sind. Wir haben nun folgendes bewiesen, 60 ist 2 x 2 x 3 x 5,
was alles Primzahlen sind. Wir haben hiermit ein mathematisches Prinzip „entdeckt“, welches Mathematiker unter dem Namen „Primfaktorzerlegung“ kennen. Jede Zahl ist zwangsläufig aus Primzahlen, die miteinander multipliziert werden,
aufgebaut – es sei denn, sie ist selbst eine Primzahl.
Listing 8: Beschränkung der Teiler auf Primzahlen
Kurze Erklärung der Codezeilen: Die innere Schleife läuft nun lediglich die bereits gefundenen Primzahlen in der
ArrayList primes als „foreach“ Schleife ab und testet sie als möglichen Teiler mit der Modulorechnung. Vorher prüfen wir aber noch, ob der aktuell geprüfte Teiler unterhalb der „Wurzelgrenze“
sqrt(i) ist. Wenn nicht, brechen wir ab. Da wir nun keine Zählschleife mehr innen haben, müssen wir dies über ein
break realisieren. Beim ersten Durchlauf ist zwar in
primes kein Wert vorhanden, dieser wird aber mit dem Wert 2 durchgeführt. Da
isPrime mit
true initialisiert wird, fügt der Algorithmus die initiale 2 also korrekt in die
ArrayList primes hinzu.
Lassen wir nun diesen Code laufen, haben wir eine Durchlaufzeit von ca. 1000 Millisekunden erreicht – also eine Verbesserung um ca. Faktor 10. Rekapitulieren wir unseren Entwicklungsprozess nochmal:
- Festlegen der Architektur.
- Definieren des Algorithmus auf Basis der Anforderung.
- Optimieren des Algorithmus basierend auf logischen bzw. mathematischen Überlegungen.
Unser Ansatz ist nun ausgereizt – mehr können wir auf den ersten Blick nicht herausholen, bis auf eine Vordimensionierung der
ArrayList auf eine zu erwartende Größe (bspw.
new ArrayList<>(maxValue/15), was einigermaßen eine innere Umschichtung der Daten in der ArrayList verhindert). Was ist aber, wenn wir von vorneherein den falschen Algorithmus gewählt haben? Ein griechischer
Mathematiker names Eratosthenes hat beispielsweise bereits ca. 200 v Chr. einen Algorithmus entworfen, der einen anderen Ansatz wählt und vor allem bei sehr großen Zahlen einen immensen Performanceschub bringt.
Die Idee ist, dass wir die Suche nach Faktoren nicht über eine Divison (bzw. Modulooperation), sondern einer Multiplikation als Umkehrung der Division durchführen. Eine Multiplikation wiederum kann auf eine Addition
zurückgeführt werden (bspw. 3x4 ist das Gleiche wie 4 + 4 + 4). Diese Tatsache können wir uns zunutze machen. Beginnen wir mit der kleinsten, bekannten Primzahl, der 2. Jedes Vielfaches von 2 kann keine Primzahl
sein, da die 2 ja als Faktor enthalten ist. Wir können also durch einen Zähler mit Schrittweite 2 alle Vielfachen von 2 als „nicht Primzahl“ markieren:

Abb.: 4: Vielfache von 2 markieren
Nun können wir die nächste Zahl für unseren Zähler verwenden, die 3:

Abb.: 5: Vielfache von 3 markieren
Die nächste Zahl für die Markiersprünge wäre nun die 4. Aufgrund unserer Primfaktorenüberlegung von oben ist dies aber nicht mehr notwendig – wir haben ja schon die 2 geprüft.
Der nächste Schritt wäre somit die nächste Primzahl, also die 5:

Abb.: 6: Vielfache von 5 markieren
Nun, da wir den Algorithmus verstanden haben, müssen wir uns Gedanken über die Datenhaltung machen. Wie schaffen wir es also, diese Information der „Markierung“ in den Rechner zu übertragen. Hier bietet sich das
Array an. Wir erweitern hier jedoch die Art und Weise, wie wir Arrays nutzen. Wir speichern in dem Array lediglich die Information ob die Position, welche die eigentliche Primzahl repräsentiert, eine Primzahl ist
oder nicht. Dadurch benötigen wir aber ein Array, welches genauso lang sein muss, wie die Maximalzahl und einfach nur ein „ja“ oder „nein“ beinhalten darf – sprich
boolean. Wir erhöhen also den Speicherbedarf massiv! Sehen wir uns diesen Algorithmus nun mal als Struktogramm an und besprechen die Funtionalität im Nachgang:
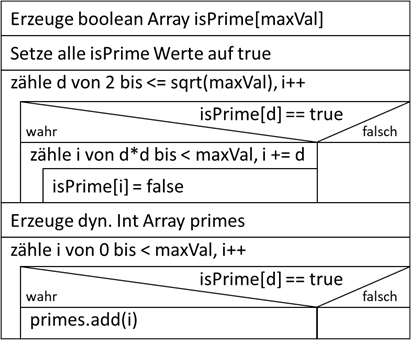
Abb.: 7: Sieb von Eratosthenes
Zuerst erzeugen wir unser Markierungsarray. Da wir es
„isPrime“ getauft haben, müssen wir zuerst alle Elemente auf
true setzen, da wir ja die „nicht Primzahlen“ über die Markierung herausnehmen möchten. Nun gehen wir die Faktoren durch – beginnend mit 2, wieder bis zur Wurzel des Maximalwertes. Hierbei prüfen wir, ob unser
aktueller Faktor eine Primzahl ist, da wir nur in Primzahlschritten die „nicht Primzahlen“ markieren müssen. Diese Prüfung ist aber mit einer einfachen Abfrage auf
„true“ getan, da in unserem Array ja genau das steht – wer ist Primzahl und wer nicht. Wenn es sicht um eine Primzahl handelt, dann beginnen wir mit dem Quadratfaktor. Dies ist deshalb sinnvoll, da alle kleineren
Faktoren bereits markiert wurden. Wenn bspw. unser Faktor aktuell die 7 ist, dann ist 2x7, 3x7 und 5x7 bereits wegen den kleineren der beiden Zahlen markiert worden. Der erste Faktor mit 7 der also zu prüfen ist,
wird die 7 x 7 sein. Damit wir das Ergebnis am Ende in der gleichen Form haben wie in dem alten Algorithmus, übertragen wir die Zahlen von dem neuen
boolean[] Datenformat in ein dynamisches Array. Sehen wir uns den zugehörigen Code in Java an:
Listing 9: Sieb von Eratosthenes in Java
Lassen wir den Algorithmus mit 10.000.000 laufen, erhalten wir eine Durchlaufzeit von ca. 110 Millisekunden. Somit haben wir durch den Strategiewechsel im Algorithmus eine Verbesserung von ca. 1100 auf 110 Milisekunden erreicht.
Wenn wir nun zum Vergleich unseren Algorithmus aus
Listing 3 nochmal mit 10.000.000 Werten laufen lassen, erhalten wir sogar eine Laufzeit im Stundenbereich. Die Frage ist nun, warum wir mit dem neuen Algorithmus eine derartige Laufzeitverbesserung haben. Zum einen verzichten
wir auf die Modulorechnung und ersetzen sie durch eine Addition, welche in puncto Rechenaufwand bei manchen Systemen die günstigere Rechenart sein kann. Je nach Prozessor kann das viel oder wenig ausmachen. Der aber wohl wichtigste
Teil ist, dass wir die Anzahl der Aktionen drastisch reduzieren. Zählen wir im Moduloverfahren aus
Listing 8 die Anzahl der Modulooperationen und im Siebverfahren aus
Listing 9 die Anzahl der Additionen und tragen sie als „Tasks“ an, können wir die Ursache des Zeitverbrauches deutlich sehen:
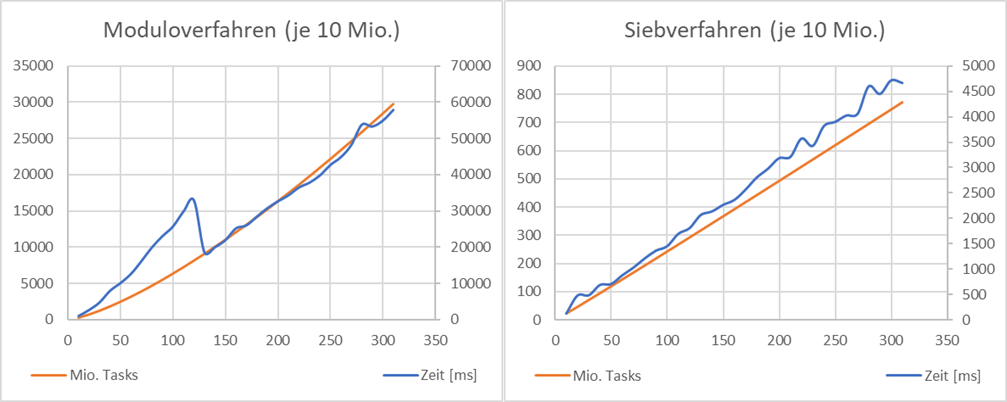
Abb.: 8: Performancevergleich Primzahlenermittlung
Wir sehen hier bei dem Moduloverfahren, dass die Anzahl der notwendigen Operationen nicht linear mit der Erhöung der Obergrenze steigt. Weiterhin erkennen wir, dass die in Summe der Operation um ca. den Faktor 40 höher liegt.
An dem gesamten Beispiel der Primzahlermittlung erkennen wir also, dass das Finden eines zeitoptimalen Algorithmus nicht immer trivial ist und mitunter mehrere Iterationsschritte bedarf. Es ist nun glücklicherwiese so, dass
wir in vielen gängigen Algorithmen entweder auf bereits existierende Bibliotheken zurückgreifen können oder wie im Beispiel der Primzahlenermittlung auf die Erfahrung anderer bauen – auch wenn diese bereits 1800 Jahre alt sind.

Sortieralgorithmen
Zum Schluss des Themas „Performance“ müssen wir noch über eine typische Algorithmusaufgabe von Computern sprechen, ohne die dieses Kapitel nicht komplett wäre – dem Sortieren von Werten. Es gehört zugegebenermaßen nicht zu
den Hauptaufgaben von Programmierern, solche Algorithmen selbst zu schreiben, da wir hierfür im Regelfall auf vorhandene Bibliotheken zurückgreifen, welche das Ganze bereits sehr schnell und effektiv lösen. Trotzdem möchte
ich hierauf eingehen, da man zumindest ein paar Grundlagen für die Sortierung verstehen sollte. Ich werde für die Erläuterungen die Sprache Java wählen, wobei es jede andere auch getan hätte. Beginnen wir mit dem
Standard-Problem der Sortierung. Wir haben eine Liste von zufälligen Werten und wollen sie absteigend oder aufsteigend sortiert haben. Hierzu bieten sich diverse Sortieralgorithmen an, welche bezüglich ihres Ressourcenbedarfs
(Speicher, CPU bzw. Zeit) unterschiedlich gestrickt sind. Ich werde mich hier lediglich auf zwei Verfahren konzentrieren – obwohl es sehr viel mehr zur Auswahl gäbe. Unser Beispiel soll nun aus sechs unsortierten Elementen
eine sortierte Liste erstellen:
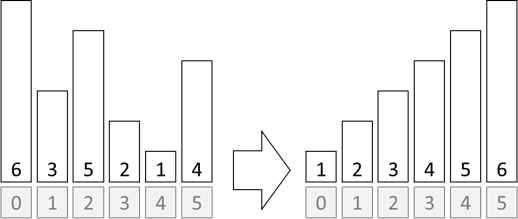
Abb.: 9: Sortieren von Werten
Wenn wir als Menschen nun diese Sortierung vornehmen, würden wir uns einen Überblick verschaffen und dann möglichst strategisch die Elemente neu anordnen. Das kann aber ein Computer so nicht umsetzen. Das Problem ist, dass er
immer nur eine Sache machen kann – wie bspw. Vergleichen. Er kann also immer nur zwei Werte gegenüberstellen – nicht die ganze Liste betrachten! Beginnen wir also mit einem ganz einfachen Gedanken. Der Rechner vergleicht einfach
die beiden linken Elemente – also die auf Indexposition 0 und 1. Wenn nun der größere vor dem kleineren steht, dann sollte er sie vertauschen. Ansonsten belässt er die Liste, wie sie ist. Im nächsten Schritt vergleicht er die
Position 0 mit der 2 und tauscht wieder. Das wird solange wiederholt, bis er alle Elemente mit der Indexposition 0 verglichen hat. Das zwingende Ergebnis ist nun, dass das kleinste Element nun an Position 0 stehen muss. Nun
macht er das gleiche mit der Indexposition 1 und so weiter. Am Ende muss er nur noch Indexposition 4 mit 5 vergleichen und ist fertig. Sehen wir uns das mal als Struktogramm an:
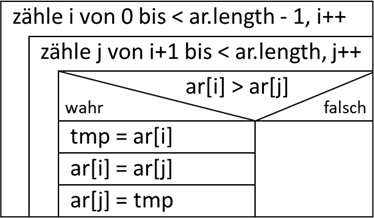
Abb.: 10: Sortieralgorithmus als Struktogramm
Das Tauschen von zwei Werten im Array erfolgt über die drei Schritte im Wahrzweig. Man legt ein Ergebnis in einer temporären Variablen ab, kann den Wert im Array nun mit dem neuen Wert überschreiben und schreibt den Wert aus der
temporären Variablen auf die neue Position. Das Ganze trägt auch den Namen „Dreiertausch“. Setzen wir den Algorithmus nun in Java um:
Listing 10: Selectionsort in Java
Wenn wir den Algorithmus laufen lassen und in jedem Durchlauf das Array ausgeben, sehen wir die fortschreitende Zuordnung der kleinsten Werte auf die linken Arraypositionen:
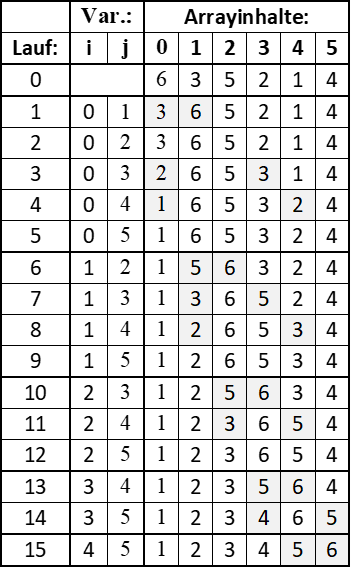
Abb.: 11: Wechsel der Werte beim Sortieren
Unser kleiner Algorithmus funktioniert also. Nun ist es zwar eine relativ „naive“ Umsetzung eines Sortieralgorithmus, aber ein einfach nachvollziehbarer. Dieser Algorithmus hat auch einen Namen bekommen – es handelt
sich um den „Selection Sort“ – da der kleinste Wert der aktuell nicht sortierten Teilliste (also die rechte Teilliste) selektiert und nach vorne getauscht wird. Wenn wir den Algorithmus nun über eine größere Anzahl von
Zahlen laufen lassen, können wir einen Zusammenhang zwischen Zeit und Anzahl feststellen:
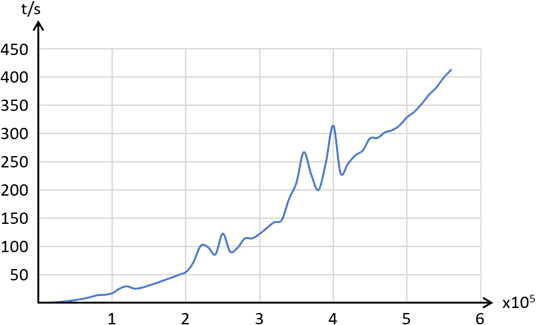
Abb.: 12: Laufzeiten Selectionsort über die Arraygröße
Wenn wir die Ausreißer, die aufgrund „Nebenbeschäftigungen“ meines Rechners entstehen, mal ausgleichen sehen wir, dass die Laufzeit über die Arraygröße keine lineare Funktion, sondern eher eine quadratische Form annimmt,
weshalb dieser Sortieralgorithmus in der Praxis praktisch keine Rolle spielt.
Einen anderen Weg geht der „Quicksort“ Algorithmus. Hier wird ein abstrakterer Ansatz gewählt. Man hat eine Liste unsortierter Elemente. In dieser Liste sucht man sich ein beliebiges Element aus. Der Einfachheit wählt
man das an der letzten Stelle. Nun sucht man die Position im Array, an der dieses Element hingehört. Hierbei prüft man von links kommend, ob alle Elemente tatsächlich kleiner als das Referenzelement ist und von rechts
kommend, ob alle größer sind. Hat man links einen zu großen Wert und rechts einen zu kleinen gefunden, tauscht man diese aus. Wenn nun die von links und rechts kommenden Prüfungen an einem Punkt treffen, muss genau an
dieser Stelle das Referenzelement platziert werden – schließlich haben wir dafür gesorgt, dass alle kleineren Elemente links und alle größeren rechts stehen. Nun kann man mit den Teilmengen links und rechts von dem neu
platzierten Referenzelement das Gleiche wiederholen, bis jede Teilmenge nur noch zwei Elemente beinhaltet. Sehen wir uns die Platzierung eines Referenzelementes in einem Beispiel an:
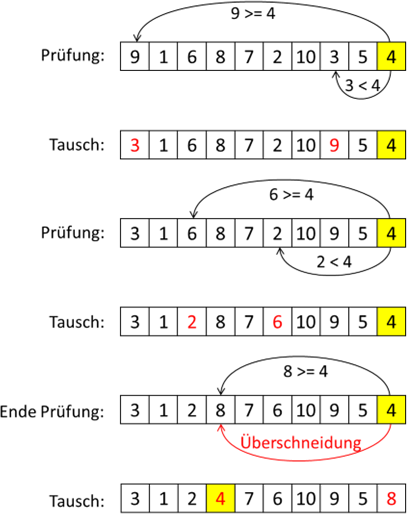
Abb.: 13: Platzierung der Referenzzahl auf die richtige Position
Nun wissen wir, dass die Referenzzahl richtig positioniert ist und wir können die Teile links bzw. rechts dieser Referenzzahl genauso verarbeiten, bis die gesamte Liste sortiert ist. Neben dem hier dargestellten Verfahren
gibt es noch andere, welche die Positionierung übernehmen. Wer Beispielimplementierungen für Quicksort sucht, wird diese Alternativen schnell finden. Das Besondere an dem Quicksort Ansatz ist nun, dass wir den Algorithmus
rekursiv gestalten, und die einzelnen Teilmengen auch noch parallelisiert verarbeiten lassen können – die Sortierung also multithreaded sein kann. Das Thema „Multithreading“ werden wir im nächsten Kapitel näher betrachten.
Setzen wir den Algorithmus nun in Java um. Wir haben hier eine sehr elegante Möglichkeit, die Verarbeitung rekursiv durchzuführen, da die Zerlegung der Liste von oben nach unten machbar ist:
Listing 11: Quicksort in Java
Kurze Erklärung der Codezeilen: Die Methode
quickSort() ist der Einstieg in das Programm. Beim ersten Aufruf aus der
main-Methode wird
left auf 0 und
right auf die Arraylänge – 1 gesetzt. Alle weiteren Aufrufe werden rekursiv gemacht. Da wir nicht immer gleichgroße Teilmengen haben, müssen wir zuerst prüfen, ob die linke und rechte Grenze sich nicht schon
berühren – sprich wir eine leere Teilmenge haben. Wenn nicht, wird die Referenzzahl über ein eigenes Unterprogramm ermittelt. Nachdem wir die Position der richtig platzierten Referenzzahl erhalten haben, rufen wir die
quickSort() Methode wieder rekursiv auf – für jede Teilmenge mit den entsprechenden angepassten Grenzen. Das Unterprogramm zur Ermittlung der Referenzposition und somit der Teilmengen besitzt je eine Variable für die
linke und rechte Grenze, wobei die rechte Variable auf der vorletzten Position beginnt. Die Referenzzahl wird nun vom rechten Rand genommen und die Schleife für die Suche nach der korrekten Position der Referenzzahl
gestartet. Nun wir von links und rechts jeweils eine „falsch positionierte“ Zahl gefunden – also von links eine zu große (oder gleich große) und von rechts eine zu kleine Zahl. Achtung – die Logik ist hier „invertiert“.
Wir laufen bspw. für
iL (also von links) solange weiter, solange alle Zahlen kleiner sind und stoppen, wenn sie größer oder gleich der Referenzzahl ist. Wenn die beiden Suchen jeweils einen Treffer gelandet haben, werden die beiden Zahlen
getauscht. Die Suche nach „falsch positionierten“ Zahlen läuft solange, bis wir die Suche von links und rechts auf dem gleichen Punkt gelandet sind. Zum Schluss wird die Referenzzahl auf die korrekte Position getauscht.
Dies darf aber nur dann geschehen, wenn die Referenzzahl nicht bereits auf der korrekten Position sitzt.
Lassen wir den Algorithmus nun wieder verschieden große Zahlenmengen verarbeiten, so sehen wir hier einen linearen Zusammenhang zwischen Anzahl der Elemente und der Verarbeitungszeit. Hier sei im Vergleich zur
Abbildung 12 nochmal auf die Achsenbeschriftungen hingewiesen – die Zeitachse ist bei Quicksort nicht in Sekunden, sondern Millisekunden, wodurch wir bei
5x105 Elementen bei ca. 50 ms und beim Selectionsort bei 325 Sekunden (!) landen – also ca. das 6500 – Fache.
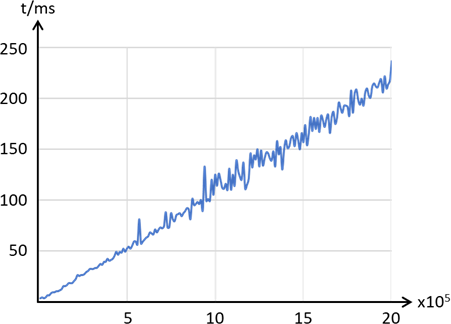
Abb.: 14: Rechenzeit über Arraygröße bei Quicksort
Nun habe ich oben erwähnt, dass solche Sortieralgorithmen bereits in den meisten Programmiersprachen fix und fertig implementiert sind und wir uns eigentlich darüber keine großen Gedanken machen müssen. In Java
würden wir ein Array bspw. mit folgendem Code sortieren:
Listing 12: Sortierung mittels Array Bibliothek in Java
Wir erhalten hier noch kürzere Laufzeiten wie mit Quicksort, da es ein erweitertes Quicksortverfahren ist, welches mehr als nur eine Referenzzahl (Pivotzahl) nutzt:
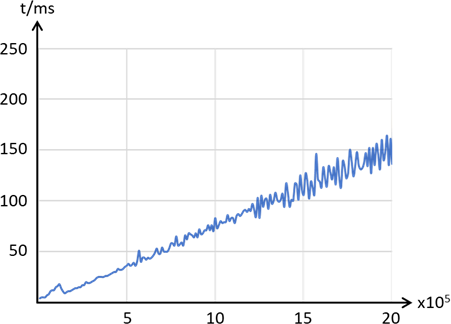
Abb.: 15: Rechenzeit über Arraygröße für dual Pivot Quicksort
Soweit ist das jetzt schon sehr praktisch. Nun haben wir aber ein kleines Problem. Wenn wir nicht direkt die Zahlen sortieren wollen, sondern Objekte nach gewissen Eigenschaften. Sehen wir uns folgende Klasse mal an:
Listing 13: Klasse, dessen Objekte sortiert werden sollen
Wir haben also eine Klasse von Personen, welche wir der (Körper)-Größe nach sortieren wollen. Wenn wir dies nun in unserem Hauptprogramm versuchen:
Listing 14: Versuch, die Personen zu sortieren
…erhalten wir eine Fehlermeldung, dass die Klasse nicht in
„Comparable“ gecastet werden kann. Intern scheint also unser Sortieralgorithmus zu versuchen, die Objekte in eine Klasse (oder besser Interface) vom Typ
Comparable zu casten. Wenn wir uns die Definition des Interfaces
Comparable mal ansehen, wird dort eine einzige Methode gefordert:
int compareTo(Object o). Diese Methode erwartet ein Objekt einer Klasse
„Type“ und muss ein
int zurückgeben. Für das aufsteigende Sortieren gelten folgende Regeln:
| Rückgabewert: | Bedingung: |
|---|---|
| Negative Zahl | Die eigene Größe muss kleiner sein als die Größe von o. |
| Positive Zahl | Die eigene Größe muss größer sein als die Größe von o. |
| 0 | Die eigene Größe ist gleich der Größe von o. |
Tabelle 2: Vergleichsbedingungen für das Comparable Interface
Wir müssen also in unserer Personen Klasse diese Methode implementieren, damit der in Java umgesetzte Sortieralgorithmus den Vergleich durchführen kann. Ergänzen wir also unsere Klasse:
Listing 15: Klasse, dessen Objekte sortierbar sind
Kurze Erklärung der Codezeilen: Über
implements Comparable müssen wir nun die Methode
compareTo() umsetzen. Hierbei müssen wir zuerst das übergebene Objekt der Klasse
„Object“ in ein Objekt der Klasse
„Person“ casten. Dies ist deshalb möglich, da während der Ausführung
Arrays.sort(personen) im Hauptprogramm nur Elemente des Arrays
personen miteinander vergleicht – und das sind alles Objekte der Klasse
Person. Nun setzen wir die Anforderung der Vergleiche um und geben jeweils -1, +1 bzw. 0 zurück.
Starten wir nun unser Programm, sehen wir die korrekt sortierte Ausgabe:
Man mag nun meinen, dass das alles recht umständlich ist. Diese Vorgehensweise ist aber zwingend notwendig, da der Computer ja nicht wissen kann, dass wir unsere Personenliste der Körpergröße nach sortieren wollen.
Wenn wir unsere Sortierbarkeit nach den Vornamen umsetzen wollen, müssten wir unsere
compareTo() Methode anders realisieren, indem wir die bereits existierende
compareTo() Methode der
String Klasse verwenden:
Listing 16: Umstellung von compareTo() auf Stringvergleich
Lassen wir nun unseren Code laufen, erhalten wir:
Wir können also somit selbst bestimmen, wie Objekte unserer eigenen Klasse sortiert werden sollen. In anderen Sprachen gibt es ähnliche Lösungen. C# hat sieht bspw. das Interface
IComparer vor. Die zu lösende Problematik wird aber immer die gleiche sein – nach welchen Kriterien wählt der intern implementierte Algorithmus den größeren, kleineren oder gleichwertigen Vergleichspartner aus.

CC Lizenz (BY NC SA)
