Damit sich was ändert: Operatoren
In den vorausgegangenen Kapiteln haben wir schon diverse Operatoren kennengelernt. Wir haben Werte zugewiesen, gerechnet und sogar schon Bitshift Operatoren angewendet. Es wird also Zeit, diese Themen strukturiert anzugehen.
Operatoren dienen dazu, Werte von (meist primitiven) Datentypen zu verändern oder miteinander zu verknüpfen. Dabei unterscheiden wir die Operation, die Operanden und den Operator. Sehen wir uns mal ein denkbar einfaches Beispiel an:
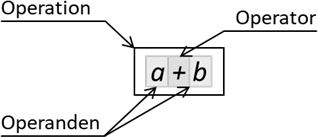
Abb.: 1: Aufbau einer Operation am Beispiel Addition
Die gesamte Operation ist also eine Addition. Der Operator wird symbolisiert durch das + und die beiden Summanden a und b, sind die Operanden. Eine vielleicht noch einfachere Operation ist die Zuweisung, welche wir üblicherweise als
„=“ Zeichen im Programm hinterlegen:
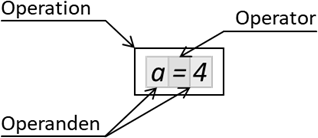
Abb.: 2: Aufbau einer Operation am Beispiel Zuweisung
Operanden können also auch Konstantwerte sein. Nun haben wir aber oftmals folgende Konstrukte vor uns:
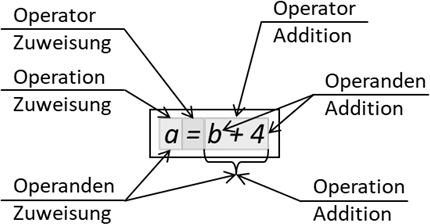
Abb.: 3: Mehrere Operationen in einer Zeile
Wir haben hier zwei Operationen, welche in einer Zeile ausgeführt werden – eine Addition und eine Zuweisung. Wichtig an dieser Stelle ist immer zu verstehen, in welcher Reihenfolge die Operationen ausgeführt werden. In unserem Fall
ist dies relativ einfach – wir addieren zuerst b und 4. Danach schreiben wir das Ergebnis in die Variable a. Diese Operationen sind nicht zu verwechseln mit Mathematischen Gleichungen! Formulieren wir diese doppelte Operation nochmal
allgemein: „Addiere den ersten und zweiten Summanden und schreibe danach das Ergebnis in a.“ Mit diesem Wissen sehen wir uns nun folgendes Konstrukt an:
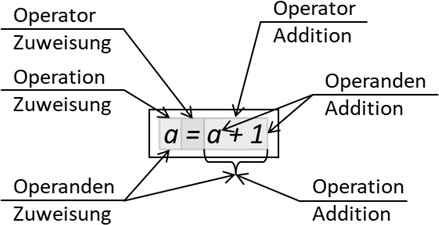
Abb.: 4: Inkrement mittels a = a + 1
Wenden wir also den gleichen Satz an: „Addiere den ersten und zweiten Summanden und schreibe danach das Ergebnis in a“ bzw. anders ausgedrückt: „Addiere den Wert, der in a steht mit 1 und schreibe danach das Ergebnis wieder in a“. Wenn
wir allerdings dieses Konstrukt mathematisch interpretieren würden, kommt eine falsche Aussage heraus, da a niemals gleich a + 1 sein kann. Wir merken uns also: Operationen sind Handlungsanweisungen und keine mathematischen Gleichungen.
Unser Konstrukt aus Abbildung 4 beinhaltet also zwei Operationen mit insgesamt 3 (plus einem „virtuellen“, nämlich das Ergebnis von a + 1) Operanden und würde dazu führen, dass der Wert in a um
eins erhöht wird. Das gleiche Ergebnis kann ich nun mit folgender Operation erreichen, welche nur zwei Operanden hat:
a += 1
Wir haben hier eine kombinierte Zuweisung, in der wir den Wert von a einfach um den Wert des rechten Operanden – in unserem Fall 1 – erhöhen. Da dies aber eine sehr häufig verwendete Operation ist, gibt es hierfür einen eigenen Operator,
den Inkrementoperator ++:
a++
Wir sehen also, dass eine Operation mindestens einen Operanden benötigt. Bei solchen, die exakt einen Operanden benötigen, spricht man von „unären“ Operatoren. Die meisten Operationen benötigen zwei Operanden (binäre Operatoren),
es gibt aber auch Operationen, welche drei Operanden erfordern (ternäre Operatoren). Weiterhin muss uns klar sein, dass wir für jeden Operator ein möglichst eindeutiges Zeichen benötigen. „Möglichst eindeutig“ heißt in diesem Zusammenhang,
dass es Operatoren gibt, welche nur auf bestimmten Datentypen sinnvoll funktionieren. Die Addition macht beispielsweise bei einem String keinen Sinn. Insofern können wir bei Zahlen das „+“ für die Addition verwenden, für Strings können wir
den „+“ Operator mit einer anderen Funktion belegen, wie bspw. in Java, wo wir mit „+“ Strings verketten.
Wir werden uns nun diesem Thema insofern nähern, als dass wir erstmal sehen, welche Kategorien von Operanden wir erwarten können. Die wichtigsten wären:
Wie immer, können wir nie 100% sicher sein, dass wir alle Operatoren kennen – auch dieses Buch wird nicht alle Operatoren benennen können! Aber wir können uns trotzdem einen relativ großen Überblick über dieses Thema verschaffen.
Es gibt auch Programmiersprachen, welche den ein oder anderen Operator gar nicht kennen oder wiederum Operatoren kennen, welche es nur in dieser Programmiersprache gibt – Python ist hier immer einen zweiten Blick wert. Ich werde
hier aber erstmal alle wichtigen Operatoren ohne eine Programmiersprachenpräferenz besprechen und am Schluss die Zuordnung und eventuelle Syntaxunterschiede bei unseren üblichen Sprachen nachliefern.

Arithmetische Operatoren
Die Operatoren, welche wahrscheinlich am schnellsten als sinnvoll einleuchten, sind die arithmetischen Operatoren, welche in gewissen Grenzen auch mit den Zuweisungsoperatoren überlappen. Unter „arithmetisch“ verstehen wir die
Grundrechenarten „Addition“, „Subtraktion“, „Multiplikation“ und „Division“, wobei wir bei der Division noch die echte Division und die ganzzahlige Division unterscheiden – und damit auch noch einen Operator für den ganzzahligen
Rest der positiven Division, sprich „Modulo“ benötigen. Und hier kommen wir schon zu einem Punkt, welcher erst auf den zweiten Blick auffällt, die Datentypen. Jede Operation bewirkt etwas – beispielsweise werden zwei Werte addiert.
Dieses Additionsergebnis muss irgendwo im Rechner vorhanden sein – ob wir es dann in einer Variablen ablegen, es direkt auf der Konsole ausgeben oder (auch wenn es sinnlos wäre) gar ignorieren – innerhalb des Prozessors wird ein
Ergebnis erzeugt und dieses wird zumindest in einem Register temporär vorhanden sein. Da der Rechner nun mal binär arbeitet, muss für dieses Ergebnis aber auch ein Datentyp existieren, damit die Interpretation des zwangsweise in
Binärcode vorliegenden Ergebnisses bei der Weiterverarbeitung sichergestellt ist. Es ist jetzt einigermaßen nachvollziehbar, dass wenn wir zwei
int Werte addieren das Ergebnis auch vom Typ
int sein sollte. Interessanter wird es aber, wenn wir dividieren. Die Rechnung 1 dividiert durch 2 gibt ja bekanntlich 0.5, aber das ist wiederum nicht mit einem Datentyp für ganze Zahlen darstellbar.
Also was passiert nun? Versuchen wir das Ganze mal in C:
Listing 1: Division ganzer Zahlen in C
Kurze Erklärung der Codezeilen: Die beiden Zahlen 1 und 2 werden als Konstanten und somit in C als
int Werte verarbeitet. Da wir eigentlich 0.5 erwarten, schreiben wir das Ergebnis in eine
double Variable und geben sie als gleitkommaformatierte Zahl aus.
Starten wir den Code, sehen wir:
Was ist also hier passiert? Der Rechner hat sich an die Regel gehalten, wenn wir zwei gleiche Datentypen verrechnen, ist das Ergebnis von genau diesem Datentyp – in unserem Fall bedeutet dies „int dividiert durch int ergibt wieder int“.
Da der ganzzahlige Wert von dem eigentlich erwarteten Ergebnis 0.5 aber die 0 ist, wird bei der Berechnung von 1 dividiert durch 2 das Ergebnis 0 sein, welches im zweiten Schritt für die Zuweisung verwendet wird. Mit anderen Worten dadurch,
dass wir zwei Operationen haben – die Divison und danach die Zuweisung, erhält die Variable
d, welche ja vom Typ
double ist, bereits den „falschen“ Wert, die 0. Dies gilt für alle statisch typisierten Programmiersprachen! Wie sieht es dann aber für dynamisch typisierten Programmiersprachen aus? Nun, bei JavaScript ist klar, dass die 0.5 rauskommen muss,
da der „Number“ Datentyp, welcher für ganzzahlige Werte und Gleitkommawerte verwendet wird, eigentlich ein
„double“ Datentyp ist. Folgender JavaScript Code gibt also die 0.5 aus.
Listing 2: Division ganzer Zahlen in JavaScript
Wenn wir nur den ganzzahligen Wert der Division haben wollen, so müssen wir das Ergebnis mit
floor(d) nachbearbeiten. Wie sieht das Ganze aber nun in Python bzw. PHP aus, wo wir ja trotz fehlender „offizieller“ Typisierung den einzelnen Werten Datentypen zuordnen können:
Listing 3: Division ganzer Zahlen in Python
Diese beiden Programmiersprachen verhalten sich wie JavaScript und geben jeweils auch die 0.5 aus. Wir sehen hier also einen systematischen Unterschied zwischen unseren Skriptsprachen und den kompilierten Sprachen, welche ja
statisch typisiert sind. Da gerade bei mathematischen Problemstellungen die ganzzahlige Division öfters benötigt wird, sahen sich daher die Python Entwickler gezwungen, hierfür ein eigenes Rechenzeichen zu definieren, das
„//“. Führen wir also den folgenden Code aus, erhalten wir wieder die 0:
Listing 4: Ganzzahlige division ganzer Zahlen in Python
Sehen wir uns nun nochmal das „modulo“ – sprich den Rest der positiven ganzzahligen Division an, was ja weiter oben schon kurz besprochen wurde. Folgender Code liefert uns in allen hier behandelten Sprachen zuverlässig die 4
(hier am Beispiel JavaScript):
Listing 5: Restoperation in JavaScript
Interessanterweise liefern uns die meisten Programmiersprachen auch ein Ergebnis, wenn wir anstatt
14%5 die Operation
14.5%5 angeben. Sinnvollerweise ist dies bei JavaScript, Java, Python C# die 4.5. PHP würde hierbei jedoch die 4 liefern, da intern das Ergebnis der Modulooperation automatisch auf
int konvertiert wird. C und C++ akzeptieren bei Modulo jedoch ausschließlich ganzzahlige Operanden.
| Operation: | Funktion: | Notation: | C: | C++: | C#: | Java: | JavaScript(1): | PHP(1): | Python(1): |
|---|---|---|---|---|---|---|---|---|---|
| Addition | Addition zweier Werte a und b | a + b | X | X | X | X | X | X | X |
| Subtraktion | Subtraktion zweier Werte a und b | a – b | X | X | X | X | X | X | X |
| Multiplikation | Multiplikation zweier Werte a und b | a * b | X | X | X | X | X | X | X |
| Division | Division zweier Werte a und b | a / b | X | X | X | X | X | X | X |
| Rest/Modulo(2) | Rest ganzzahlige Division a und b | a % b | X | X | X | X | X | X | X |
| Potenz | a hoch b | a ** b | X | ||||||
Tabelle 1: Arithmetische Operationen
(1) Grau hinterlegt: Datentyp ändert sich ggf.
(2) Python implementiert „Modulo“ und alle anderen „Rest“ mit dem % Symbol
(2) Python implementiert „Modulo“ und alle anderen „Rest“ mit dem % Symbol
Am Beispiel der Potenz sehen wir wieder, dass Python klar auf die Mathematik abzielt. Während Python hierfür einen einfachen Operator hat, müsste man in den anderen Sprachen auf Bibliotheksfunktion wie
„pow()“ etc. zurückgreifen.
Nun müssen wir der Vollständigkeit halber noch den Unterschied zwischen „Modulo“ und „Restwertberechnung“ klären. Wie weiter oben schon erwähnt, sind beide Operationen im positiven Wertebereich gleich. Wenn wir aber negative
Werte berücksichtigen, gibt es einen Unterschied. Vergleichen wir hier mal JavaScript und Python bei der Rechnung
-14%5:
Listing 6: Restoperation in JavaScript
Das Ergebnis ist -4, da die gesamte Rechnung ja lautet:
-14 : 5 = -2, Rest -4
Führen wir das gleiche nun in Python aus:
Listing 7: Modulooperation in Python
Das Ergebnis dieses Codes lautet nun 1 – also die positive 1. Was hier umgesetzt wird ist die mathematische Modulooperation, welche folgenden Gedanken der Division aus dem positiven Zahlenbereich in den negativen überträgt: Wenn gilt
a : b = c Rest
r, dann wähle
c so, dass
c * b gerade noch kleiner als
a ist. Rest
r ist der Betrag, den man hinzuaddieren muss, um wieder auf
a zu kommen. Überlegen wir uns das mal bei 14 : 5. Ich nehme 2, da 2 mal 5 gerade noch kleiner als 14 ist:
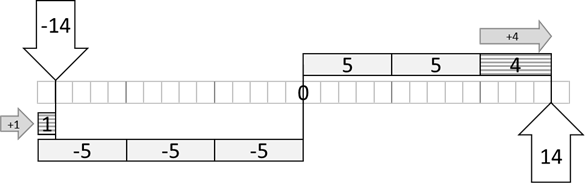
Abb.: 5: Modulo im positiven und negativen Zahlenbereich
Machen wir nun das gleiche im negativen Bereich. Wir können also bei -14 : 5 nicht -2 mit Rest nehmen, da -2 mal 5 gleich -10 ist, was ja nicht kleiner als -14 ist, sondern größer. Wir müssen also -3 mit Rest nehmen, womit wir bei -15 landen.
Nun addieren wir die „Rest 1“ hinzu und erhalten die -14. Sehen wir uns die Grafik bei der Restwertberechnung an:
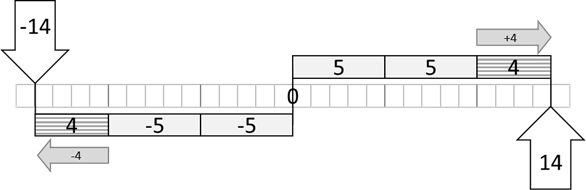
Abb.: 6: Rest bei positiven und negativen Zahlenbereich
Hier rechnen wir -14 : 5 = -2 mit Rest -4. Wie wir sehen, ist die Restwertberechnung bei positiven und negativen Zahlen symmetrisch gegenüber dem Ursprung, weshalb man die Restwertoperation mitunter auch symmetrische Modulooperation nennt.

Zuweisungsoperatoren
Die nächste Operatorengruppe bilden die Zuweisungen. Hier gibt es erstmal die offensichtliche Zuweisung von einem Wert in eine Variable:
a = 10
Wichtig ist hier, dass die Zuweisung von rechts nach links erfolgt, was bedingt, dass der linke Operand änderbar sein muss. Eine weiter oben
beschriebene Eigenschaft des Zuweisungsoperators ist, dass eine Klammer um die Zuweisung den zugewiesenen Wert annimmt. Hier an einem Java
Beispiel:
Listing 8: Zuweisung in Klammern in Java
Kurze Erklärung der Codezeilen: Die erste Zeile ist lediglich dafür da um zu beweisen, dass der Wert 1 im Folgenden überschrieben wird.
In der zweiten Zeile wird die erste Zuweisung in den Klammern ausgeführt:
i = 3, wodurch
i den Wert 3 erhält und 1 überschrieben wird. Nun wird die Klammer mit dem Wert 3 ersetzt, so dass die verarbeitete Codezeile zu
int j = 3 + 2 wird.
Das Ergebnis auf der Konsole ist somit 3 5. Solche Konstrukte kann man oft bei Schleifen finden, wenn wir einen Codeblock solange ausführen
müssen, solange bspw. ein Wert ungleich 0 übergeben wird:
while((i = wert) != 0); Allerdings wird dieses Konzept nicht von allen Programmiersprachen unterstützt, bzw. macht diese Nutzung den Code
schwer lesbar. Bspw. würde in Python wegen dem Verzicht auf Klammern der Code aus
Listing 8 wie folgt notieren:
j = i = 3 + 2.
Neben diesem offensichtlichen Operator für die einfache Zuweisung gibt es aber noch weitere Operatoren, welche im Prinzip eine Zusammenfassung einer
Zuweisung und eines weiteren Operators ist. Wir haben diese Schreibform weiter oben bereits kennengelernt:
a += 10
Dieser Zuweisungsoperator ist die Kurzform von
a = a + 10 und kombiniert somit die Addition und die Zuweisung in den rechten Additionsoperanden in einer einzigen Operation. Diese Kurzform
können wir mit allen wesentlichen anderen Operatoren auch durchführen
(+=, -=, *=, /=, %=, &=, |=, ^=, <<=, >>=). Es gilt also immer:
a = a ? b wird zu a ?= b
wobei a für eine veränderbare Variable, b für einen beliebigen Operanden und ? für einen Operator steht, der die
Operanden miteinander in irgend einer Form verknüpft. Die nächsten oft genutzten Operatoren sind die sogenannten Inkrement- und
Dekrement-Operatoren
„++“ und
„--". Sie erhöhen oder verringern den Wert des Operanden um den Wert 1. Beim Einsatz dieser Operatoren gilt es aber einen wichtigen Punkt zu
beachten. Sehen wir uns hierfür folgenden Code in C# an:
Listing 9: Postinkrement Operator in C#
Kurze Erklärung der Codezeilen: Die
int Variable
i wird auf 1 gesetzt, womit der Inkrementoperator
++ aus 1 die 2 machen muss. In der zweiten Zeile, in der wir den Inkrementoperator einsetzten, greifen wir aber auch noch für die
Ausgabe lesend auf
i zu. Dies bedeutet, dass wir hier zwei Dinge machen, das Inkrement und die Ausgabe. Wir können also sehen, ob das Inkrement oder die
Ausgabe zuerst erfolgt. Danach geben wir
i nochmals aus.
Die Konsolenausgabe beweist uns nun, dass zuerst der lesende Zugriff und dann erst das Inkrement erfolgte:
Aus diesem Grunde nennen wir
i++ auch „Postinkrement“. Es gibt entsprechend auch das Pendant, den „Preinkrement“ Operator. Hier schreibt man das
++ vor den Operanden:
Listing 10: Preinkrement Operator in C#
Die Konsolenausgabe zeigt den Unterschied:
Es wird hier also zuerst erhöht und dann erst lesend zugegriffen. Leider macht Python bei den Inkrement- und Dekrement-Operatoren auch
wieder eine Ausnahme – sie werden schlichtweg nicht unterstützt. In Python muss man für Inkrement auf
i+=1 und Dekrement auf
i-=1 zurückgreifen. Insofern kommt die Frage nach Post- und Präinkrement erst gar nicht auf.
| Operation: | Funktion: | Notation: | C: | C++: | C#: | Java: | JavaScript: | PHP: | Python(3): |
|---|---|---|---|---|---|---|---|---|---|
| Zuweisung | Wert von b wird in a übernommen | a = b | X | X | X | X | X | X | X |
| Postinkrement | Erhöhung a um 1 nach Lesevorgang | a++ | X | X | X | X | X | X | |
| Postdekrement | Reduktion a um 1 nach Lesevorgang | a-- | X | X | X | X | X | X | |
| Preinkrement | Erhöhung a um 1 vor Lesevorgang | ++a | X | X | X | X | X | X | |
| Predekrement | Reduktion a um 1 vor Lesevorgang | --a | X | X | X | X | X | X | |
| Kombinierte Zuweisung | Anwendung des Operators ?(4) auf a mit b und speichern Ergebnis in a | a ?= b | X | X | X | X | X | X | X |
Tabelle 2: Zuweisungsoperationen
(3) Python kennt zwar den Operator ++a, jedoch wird er nicht als Preinkrement ausgeführt
(4) ? ist ein Platzhalter und steht für +, -, *, /, %, &, |, ^, <<, >>
(4) ? ist ein Platzhalter und steht für +, -, *, /, %, &, |, ^, <<, >>

Vergleichsoperatoren
Eine weitere Operatorengruppe, welche wir teilweise schon angewendet haben, sind die Vergleichsoperatoren. Ein Vergleich kann immer nur
true oder
false sein. Insofern haben Vergleichsoperatoren ein
boolean Ergebnis. Da in machen Programmiersprachen
true/false auch über 1/0 dargestellt werden kann, ist es auch möglich, das Ergebnis in einer
int Variable zu speichern. Wenn wir zwei Operanden a und b haben, kennen wir im Wesentlichen die
folgenden Optionen:
| Vergleich: | Mathematischer Ausdruck: |
|---|---|
| a gleich b | a = b |
| a ungleich b | a <> b |
| a größer b | a > b |
| a größer oder gbleich b | a >= b |
| a kleiner b | a < b |
| a kleiner oder gleich b | a <= b |
Tabelle 3:Vergleichsarten
Hier gibt es erstmal ein kleines Problem. Die Prüfung auf Gleichheit würde in der Mathematik den gleichen Operator fordern wie die
Zuweisung – wir erinnern uns: eine Zuweisung ist keine Gleichung. Die Mathematik würde für eine Zuweisung eher das
:= verwenden, da das Gleichheitszeichen für den Vergleich genutzt wird. Nun gibt es Programmiersprachen,
welche aus dem Kontext ersehen, ob es sich um einen Vergleich oder um eine Zuweisung handelt, wodurch die Kombination von mehreren
Zuweisungen in Kombination mit anderen Operationen wie in Listing 8
nicht mehr umsetzbar ist. Daher lösen die meisten Programmiersprachen dieses Dilemma mit einem eigenen Vergleichsoperator, dem
doppelten Istleich:
„==“. Ein weiterer auffälliger Unterschied ist das „Ungleich“. In dem meisten Programmiersprachen ist die
Negation das Ausrufungszeichen
„!“, worauf wir später noch näher eingehen. Insofern wurde beim Vergleichsoperator das erste Istgleich mit
dem Ausrufungszeichen ersetzt, wodurch
„!=“ für „Ungleich“ entsteht. Schließlich sei noch erwähnt, dass bei JavaScript und PHP noch der Operator
für die „strikte Gleichheit“ existiert, welcher notwendig war, um einen datentypunabhängigen Vergleich mit
„===“ zu realisieren (siehe hierzu nochmal
Kapitel 10).
| Operation: | Funktion: | Notation: | C: | C++: | C#: | Java: | JavaScript: | PHP: | Python: |
|---|---|---|---|---|---|---|---|---|---|
| gleich | Gleichheit Werte(5) | a == b | X | X | X | X | X | X | X |
| ungleich | Ungleichheit Werte | a != b | X | X | X | X | X | X | X |
| strikt gleich | Gleichheit Werte und Datentypen | a === b | X | X | X | X | X | X | |
| strikt ungleich | Ungleichheit Werte oder Datentypen | a !== b | X | X | X | X | X | X | |
| größer | Linker Wert größer rechter Wert | a > b | X | X | X | X | X | X | X |
| größer oder gleich | Linker Wert größer oder gleich rechter Wert | a >= b | X | X | X | X | X | X | X |
| kleiner | Linker Wert kleiner rechter Wert | a < b | X | X | X | X | X | X | X |
| kleiner oder gleich | Linker Wert kleiner oder gleich rechter Wert | a <= b | X | X | X | X | X | X | X |
Tabelle 4: Vergleichsoperatoren
(5) Bei kompilierten Sprachen in der Regel unabhängig vom Datentyp
In Python gibt es jetzt noch einen Operator, welcher so in den anderen Programmiersprachen nur über Umwege ersetzt werden kann,
den „Identitätsoperator“
„is“, welcher prüft, ob es sich um ein und dasselbe Objekt handelt – sprich es wird ein Vergleich der Referenz (bzw. Adresse) durchgeführt.

Logische Operatoren
Um alle Details für die nächsten Operatoren zu verstehen, müssen wir uns nochmal ein physikalisches Modell für die logischen
Verknüpfungen ansehen, so wie wir sie im
Kapitel 4
gesehen haben – der Einfachheit halber mit nur zwei Eingängen. Unser Modell sieht vor, dass das Eingangssignal ein Knopf ist,
den man drücken kann. Der Zustand
„true“ ist also ein gedrückter Knopf. Dieser wiederum steuert ein Ventil in einem Rohr. Wenn dieses Ventil den Durchfluss freigibt,
dann ist das Signal „wahr“. Hier das einfachste mögliche Beispiel – Ausgang ist gleich Eingang (also Eingangssignal =
true – „gedrückt“ führt zu Ausgangssignal
true – Wasser läuft):
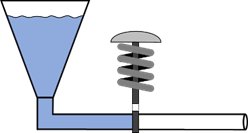
Abb.: 7: Modell einer 1:1 Durchreichung
Mit diesem Modellkonzept können wir uns nun alle Logikoperationen bildlich vorstellen. Beginnen wir mit der Negation. Hier möchte man,
dass bei einem Eingangswert
„true“ ein Ausgangswert
„false“ entsteht. Dies können wir mit folgendem Modell darstellen:
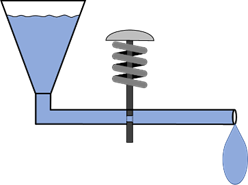
Abb.: 8: Modell einer Negation
Waren die beiden letzten Operationen jeweils mit nur einem Eingang realisiert, haben die nächsten Operationen mindestens zwei.
Wir werden noch sehen, dass in der Verarbeitung in Programmen die logischen Operationen immer nur zwei Eingänge haben – anders als in der
diskret aufgebauten Welt, wie wir sie in Kapitel 4 kennengelernt haben. Die erste
Operation ist das logische „UND“. Hier müssen immer beide Eingänge auf
„true“ sein, damit der Ausgang
„true“ ist. Für unser Modell gilt somit, die Flüssigkeit fließt dann, wenn beide Taster gedrückt sind:
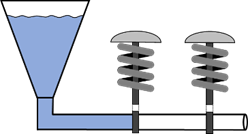
Abb.: 9: Modell einer logischen UND Verknüpfung
Beim logischen „ODER“ war die Situation, dass mindestens ein Knopf gedrückt werden muss, damit wir am Ausgang ein
„true“ haben. Dies lässt sich wie folgt modellieren:
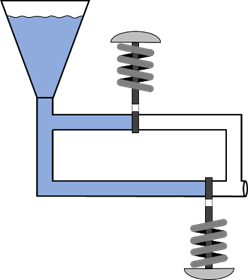
Abb.: 10: Modell einer ODER Verknüpfung
Jetzt fehlt nur noch das „Exklusiv ODER“, kurz XOR. Hier darf immer nur ein Knopf gedrückt sein, damit wir ein Ergebnis am
Ausgang haben. Eine Möglichkeit für eine modellhafte Vorstellung wäre wir folgt:
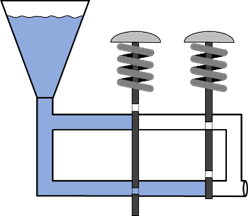
Abb.: 11: Modell einer XOR Verknüpfung
| Verknüpfung: | Symbol: |
|---|---|
| a UND b | a && b bzw. a & b |
| a ODER b | a || b bzw. a | b |
| a XOR b | a ^ b |
| a negiert | !a |
Tabelle 5: Symbole von logischen Verknüpfungen
Was zuerst auffällt ist, dass wir das
„&“ bzw. das
„|“ doppelt, bzw. einfach finden. Die beiden unterschiedlichen Notationen haben auch tatsächlich ein
unterschiedliches Verhalten, obwohl die Operatoren einfach bzw. gedoppelt jeweils ein UND und ein
ODER abbilden. Hier müssen wir uns jetzt an unser Modell erinnern. Beginnen wir mit der UND Verknüpfung und
sehen uns das Modell in
Abbildung 9 an. Gehen wir mal davon aus, dass der Abfluss unseres
Konstrukts irgendwo ganz weit weg ist, so dass wir ihn nicht sehen können. Wir möchten aber feststellen,
ob Flüssigkeit durch unser Rohrsystem fließt oder ob es blockiert ist. Wir prüfen also unseren ersten Knopf
und stellen fest, dass er nicht gedrückt ist. Es ist nun nicht mehr notwendig, den zweiten Knopf zu prüfen –
da niemals Flüssigkeit fließen wird, wenn eben einer der beiden Knöpfe nicht gedrückt ist. Erst wenn wir
feststellen, dass der erste Knopf gedrückt ist, sollten wir den zweiten prüfen. Da nun unser Rechner sequenziell
unser Programm abarbeitet, hat er im Prinzip die gleiche Möglichkeit. Wenn also eine UND Verknüpfung vom
Prozessor geprüft wird, so kann er eigentlich aufhören, sobald er das Ergebnis bereits weiß – im Falle von
UND ist das, sobald ein Operand den Wert
„false“ hat. Um dies zu prüfen, probieren wir folgenden Java Code aus:
Listing 11: Analyse doppelter UND Operator
Kurze Erklärung der Codezeilen: Die
int Variablen
i und
j werden auf 1 bzw. 0 gesetzt und in der Verzweigung auf 0 geprüft. Die beiden Prüfungen verknüpfen wir
mit dem doppelten UND Operator. Den rechten Operanden erweitern wir aber mit einem Postinkrement auf dem
j. Dadurch können wir prüfen, ob der Prozessor die rechte Seite unser
&& Verknüpfung überhaupt verarbeitet, oder vorher abgebrochen hat.
Die Variable
j wurde also nicht um 1 erhöht, was uns zeigt, dass der Prozessor nur die erste Prüfung durchgeführt hat.
Ändern wir nun die Bedingung von
if (i == 0 && j++ == 0) auf
if (i == 0 & j++ == 0), so erhalten wir die Ausgabe:
Jetzt hat der Prozessor beide Seiten der Verknüpfung verarbeitet, obwohl er die rechte Seite nicht hätte
prüfen müssen. Dieses Verhalten, dass beim
„&&“ Operator die Prüfung abgebrochen wird, sobald das Ergebnis feststeht, nennen wir ein „lazy“ Verhalten.
Bei der Analyse der ODER Verknüpfung in Abbildung 10 erkennen wir,
dass hier die Vorgehensweise anders sein muss. Hier können wir sagen, dass wir beim ersten gedrückten Knopf
das Ergebnis bereits wissen. Wenn also der linke Knopf gedrückt ist, fließt garantiert die Flüssigkeit.
Dies bedeutet für unseren Code, dass der Prozessor die Prüfung einer ODER Verknüpfung abbrechen kann,
sobald er ein
„true“ gefunden hat. Auch dies können wir mit unserem Java Programm untersuchen, indem wir
i mit 0 belegen und das
„&&“ durch
„||“ tauschen:
Listing 12: Analyse doppelter ODER Operator
Hier erhalten wir als Ausgabe:
Die rechte Seite wurde wieder nicht verarbeitet. Ersetzen wir wieder das
„||“ durch
| so wird der Prozessor wieder gezwungen, alles zu verarbeiten und wir erhalten:
Diese Wahl zwischen einem normalen und einem „lazy“ Verhalten haben wir bei allen Programmiersprachen, bis
auf Python. Dort nutzt man die ausgeschriebenen Operatorenbezeichnungen
„and“ und
„or“. Es gibt somit auch keine „doppelten“ oder „einfachen“ Operatoren. Python verarbeitet die beiden
Operatoren immer „lazy“. Dies ist insofern tragbar, als dass wir in den anderen Programmiersprachen ohnehin
fast ausschließlich die doppelten verwenden – sprich wir wollen, dass die Prüfung abbricht, sobald das
Ergebnis feststeht. Die einzelnen Operatoren nehmen wir nur, wenn wir die Werte in der Prüfung verändern
wollen (wie bspw. mit dem Inkrementoperator in unseren Testprogrammen oben, oder auch einem Funktionsaufruf
innerhalb der Prüfung). Dies ist allerdings keine sehr übersichtliche Art zu programmieren, insofern konnten
die Python Entwickler darauf verzichten. Das Verständnis dieses lazy Verhaltens ist nun für folgende Situation wichtig:
Listing 13: Analyse doppelter ODER Operator
Kurze Erklärung der Codezeilen: Wir haben ein Array
„ar“, welches entweder nicht vorhanden ist (also
null, so wie in dem Listing) oder ein leeres Array sein kann (dann würde stehen
int[] ar = new int[0];) oder eben ein Array mit irgendwelchen Werten (also bspw.
int[] ar = {1, 2, 3};). Wenn wir mit den Daten des Arrays arbeiten wollen, dann müssen wir sicherstellen,
dass auch Daten vorhanden sind. Mit der Prüfung auf
ar == null stellen wir fest, ob das Array existiert. Mit
ar.length == 0 prüfen wir, ob es nicht vielleicht leer ist. Diese Prüfung auf die Länge können wir aber nur
dann machen, wenn es existiert, also nicht
null ist.
Dieser Code gibt natürlich aus, dass das Array nicht vorhanden oder leer ist. Wenn wir aber aus dem
„||“ ein
„|“ machen, so würde der Code bei Ausführung eine
NullPointerException werfen, da ja beide Seiten der Verknüpfung abgearbeitet werden würden. Somit würde zwar links festgestellt werden,
dass
ar gleich
null ist, aber die Prüfung auf die Länge würde trotzdem durchgeführt werden, was zum entsprechenden Fehler führt. Der Abbruch ist also
in dieser Situation einer Prüfung auf
null absolut sinnvoll (neben der Tatsache, dass dies ein Performancevorteil ist, dann abzubrechen, wenn das Ergebnis feststeht).
Fehlt nun noch das XOR, welches als Operatorsymbol meist das Zirkumflex Zeichen
„^“ hat. Hier können wir die sequenzielle Abarbeitung des Codes am besten sehen. In diskretem Aufbau kennen wir ein XOR mit mehr als
zwei Eingängen. Unser Rechner kennt dies aufgrund der Tatsache, dass die logischen Operatoren binär sind nicht und verarbeitet somit
einfach die Werte von links nach rechts:
Listing 14: Analyse Aufrufverhalten XOR in Java
Wir erhalten hier das
„true“ am Ausgang, was für jemanden, der ein XOR mit drei Eingängen aus der Hardware kennt erstmal für Stirnrunzeln sorgen würde.
Sehen wir uns das Ganze mal aus dieser Hardwaresicht an. In Kapitel 4 sehen
wir eindeutig, dass ein XOR mit drei mal der 1 am Eingang (also drei mal
„true“) als Ausgangswert die 0 (also
„false“) erzeugt. In unserem Flüssigkeitsmodell würde also ein solches Konstrukt wie folgt aussehen:
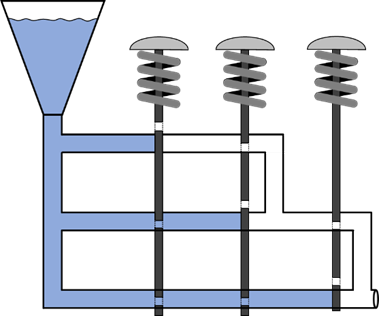
Abb.: 12: Modell eines diskreten XOR mit drei Eingängen
Es handelt sich also um eine komplexe Verschaltung der einzelnen Eingangssignale, welche exakt auf ein XOR mit drei Eingängen ausgelegt
ist. In der programmierten Variante hingegen wird das Ausgangssignal des ersten XOR (mit zwei Eingängen) als Eingangssignal des nächsten
XOR (mit zwei Eingängen) genutzt. Wir modellieren das derart, dass die Flüssigkeit aus dem ersten XOR einfach den linken Knopf des
zweiten XOR betätigt:
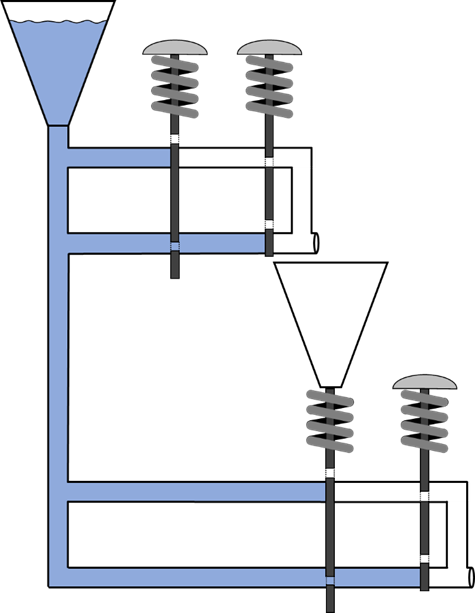
Abb.: 13: Modell eines programmierten XOR mit drei Eingängen
Wir sehen also, dass bei
„true“ gleichzeitig auf den ersten beiden Knöpfen, das erste XOR
„false“ ausgibt – sprich keine Flüssigkeit in den Behälter des dritten Knopfes fließt und dieser somit nicht betätigt wird. Drücken wir
nun den ganz rechten Knopf, so hat das untere XOR als Eingangssignale
„false“ (aus dem oberen XOR) und
„true“ aus dem rechten Knopf, weshalb es
„true“ erzeugt – sprich es kommt Flüssigkeit aus dem unteren Rohr. Dies erklärt somit auch, warum es beim XOR kein doppeltes Symbol
gibt wie bspw.
&& oder
||, da wir beim XOR erst dann den Wert des Gesamtkonstrukts wissen, wenn wir alle Eingänge berücksichtigt haben.
Der letzte logische Operator ist vermutlich der einfachste – die Negation. Der Operator steht immer vor dem Operanden und macht aus
einem
true Wert ein
false und umgekehrt. Bis auf Python nutzen alle Sprachen das Ausrufungszeichen als Symbol:
Listing 15: Negationsoperator in Java
Hier nochmal ein Überblick über die logischen Operatoren:
| Operation: | Notation: | C: | C++: | C#: | Java: | JavaScript: | PHP: | Python:(5) |
|---|---|---|---|---|---|---|---|---|
| a UND b | a && b bzw. a & b | X | X | X | X | X | X | a and b |
| a ODER b | a || b bzw. a | b | X | X | X | X | X | X | a or b |
| a XOR b | a ^ b | X | X | X | X | X | X | X |
| a negiert | !a | X | X | X | X | X | X | not a |
Tabelle 6: Logische Operatoren
(5) Python unterstützt die Operationen, jedoch teilweise mit anderen Symbolen
Abschließend zu den logischen Operatoren ist noch zu sagen, dass sie „nur“ bei
boolean Werten arbeiten. Nun sind aber die Zeichen
„&“,
„|“ und
„^“ mit unterschiedlichen Operationen belegt, je nach Datentyp der Operanden. Wir werden uns gleich die bitweisen Operationen ansehen, wo
wir diese Symbole wiederfinden. Wenn wir zwischen zwei
boolean Operanden also ein
& Zeichen finden, ist klar, was passieren wird. Bei typisierten Programmiersprachen ist das Operatorenverhalten also relativ einfach
vorhersagbar. Wie sieht das aber bei interpretieren Sprachen aus? Python löst das Ganze – zumindest bei UND und ODER – relativ einfach, indem
die Symbole
„&“ bzw.
„|“ für die bitweise Verarbeitung und
„and“ bzw.
„or“ für die logischen Operationen eingesetzt werden sollen. Doch was bedeutet „bitweise Verarbeitung“? Wir haben ja festgestellt, dass wir
den Zahlenwerten jeweils ein Bitmuster zuordnen können. So ist die Zahl 1 binär 0b1 und die Zahl 2 0b10. Wir können somit diese beiden Zahlen
untereinanderschreiben und mit einer ODER Verknüpfung „zusammenrechnen“:
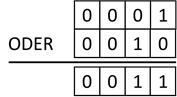
Abb.: 14: Bitweises ODER von 0b1 und 0b10
Das Ergebnis ist also für die beiden rechten Spalten die 1, wodurch 0b11 herauskommt. Dies wiederum ist in Dezimaldarstellung die 3. Dies
müssten wir nun auch als Code realisieren können:
Listing 16: Bitweises vs. logisches OR in Python
Kurze Erklärung der Codezeilen: Wir erzeugen eine boolean Variable
b mit
„True“ und verknüpfen via
or den Wert
False, was natürlich
True ergeben wird. Nun können wir aber auch den
„|“ Operator nutzen, was die Bitweise Verknüpfung des Wertes 1 in Varable
i mit dem Wert 2 abbildet, wodurch wir die 3 erwarten würden.
Die Ausgabe bestätigt dies mit:
Nun kann man in Python aber die Operatoren beliebig zusammenstellen. Sehen wir uns deshalb mal die Ergebnisse zusammen mit den
Datentypen der Ergebniswerte an:
Listing 17: Bitweises vs. logisches OR bei „falschen“ Datentypen in Python
Hier erhalten wir nun überraschenderweise:
Beginnen wir mit den Wert
b. Das
„|“ wird in Python in dieser Situation genauso verarbeitet wir das
„or“. Es ist hier auch zweitrangig, ob intern ein bitweises oder ein logisches ODER durchgeführt wird, da die Definition „alles was nicht 0
ist, ist
True“ eine bitweise Verarbeitung mit dem richtigen Ergebnis erlauben würde – vor allem wenn man die Definition umdreht.
Wenn also
„False“ 0 und
„True“ irgendeine Zahl ungleich 0, muss ein bitweises ODER zwangsweise auch eine Zahl ungleich 0 ergeben. Wichtig ist, dass das Ergebnis vom
Datentyp
„bool“ ist. Spannender ist bei unserer Konsolenausgabe bei den folgenden Ergebnissen. Beginnen wir mit der Zuweisung zu
c. Hier wird
„False“ als 0 verarbeitet und Bitweise mit der 1 verknüpft, wodurch 1 als
int herauskommt. Dass dies passiert können wir mit
d prüfen, da hier
False mit 2 bitweise verknüpft wird und 0b01 „verodert“ mit 0b10 ergibt 0b11, was dezimal die 3 ist. Bei der Variablen
e verknüpfen wir einen
bool Wert mit einem Boolean ODER Operator mit einer Zahl 1. Hier wird zuerst die linke Seite des ODER Operators ausgewertet.
False bedeutet, dass die rechte Seite ebenfalls ausgewertet werden muss. Hier steht nun eine Zahl, weshalb sich Python dafür entscheidet,
auch eine Zahl im Ergebnis zu präsentieren, was die 2 sein muss, da dies der Wert des linken Operanden ist, die 2. Da in Python das
„or“ lazy ist, können wir auch das Verhalten für die Variable
f interpretieren. Die linke Seite von
„or“ ist
„True“, weshalb die rechte Seite nicht weiter beachtet wird und der
bool Wert
„True“ ausgegeben wird. Die Variablen
i und
j sind dann lediglich Konsequenzen aus den vorausgegangenen Beobachtungen.
Eine ähnliche Untersuchung können wir nun bei JavaScript anstreben. Das
„|“ Symbol wird hier für das Bitweise und
„||“ für das logische ODER genutzt:
Listing 18: Analyse der ODER Operatoren in JavaScript
Hier erhalten wir nun überraschenderweise:
Nun, interpretieren wir diese Ausgabe. Bis auf die Variable
b haben wir identisches Verhalten zu Python, weshalb wir nur auf
b eingehen. Hier sehen wir, dass JavaScript bei einer bitweisen Verarbeitung immer eine Zahl ausgibt – unabhängig der Operanden.
Das PHP-Verhalten spare ich mir hier, da die wesentliche Aussage bis hier eigentlich klar geworden sein sollte. Wir müssen also auch bei
nicht typisierten Sprachen die dahinterliegenden Datentypen immer im Blick haben, da wir sonst die Verhaltensweisen der Operatoren nicht
immer sauber beurteilen können. In typisierten Sprachen ist dies nur dann eine Herausforderung, wenn wir die Datentypen bei einer Operation
mischen.

Bitweise Operatoren
Nun haben wir implizit schon die nächste Klasse an Operatoren eingeführt – die Bitweisen Operatoren. Diese werden in aller Regel nur sinnvoll bei ganzzahligen
Datentypen einsetzbar sein. Es gibt zwar Sprachen, welche bitweise Operatoren bei Gleitkommazahlen akzeptieren, wobei sie vor der Operation zu ganzzahligen Typen umgewandelt
werden. Inhaltlich ist es zwar nicht sinnvoll, bitweise auf Gleitkommazahlen zuzugreifen, bei nicht typisierten Programmiersprachen wissen die Programmierer oft aber nicht,
dass sie gerade mit einem Gleitkommatyp ohne Nachkommastellen arbeiten. Ein Beispiel wäre hier PHP. Andere Sprachen wiederum würden bei der bitweisen Verarbeitung von
Gleitkommatypen einen Laufzeitfehler verursachen. Insofern beschränke ich mich hier auf die Betrachtung von ganzzahligen Datentypen.
Beginnen wir wieder mit einer Aufstellung der häufigsten bitweisen Operatoren mitsamt den üblichen Symbolen:
| Bitweise Operation: | Symbol: |
|---|---|
| a UND b | a && b bzw. a & b |
| a ODER b | a || b bzw. a | b |
| a XOR b | a ^ b |
| a NICHT | ~a |
| Shift nach rechts um b Stellen | a >> b |
| Shift nach links um b Stellen | a << b |
Tabelle 7: Symbole von bitweisen Operatoren
Die Grundidee bei den bitweisen Operatoren ist, dass die Zahlen als das gesehen werden, was sie tatsächlich im Speicher sind, nämlich Einsen und Nullen. Diese werden dann
bitweise verarbeitet. Sehen wir uns das am Beispiel der UND Verknüpfung in C# an:
Listing 19; Bitweises UND in C#
Die Ausgabe ist 129. Sehen wir uns das Ganze mal als Binärzahlen an:
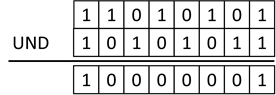
Abb.: 15: Bitweises UND
Das gleiche Konzept steht auch hinter dem bitweisen ODER und dem bitweisen XOR. Einen weiteren Blick ist hier noch die Negation wert. Wenn wir eine Zahl negieren:
Listing 20; Bitweises NICHT in C#
Das Ergebnis ist -171. Dies ist insofern nicht überraschend, da man das Zweierkomplement als Darstellung einer Zahl mit negativem Vorzeichen durch die Invertierung
aller Bits und der anschließenden Addition von 1 erhält.
Die Bitshift Operation wurde weiter oben ebenfalls schon angesprochen. Wenn wir diesen Operator anwenden, dann bedeutet
a << b, dass wir die Bits um
b nach links verschieben – was wiederum rein mathematisch die Rechnung a * 2b ist. Wir schieben das Komma im Binärsystem also um
b Stellen nach rechts. Probieren wir es mit 170 * 23 = 170 * 8 = 1360 aus!
Die Ausgabe ist wie erwartet 1360. Bitshift rechts wiederum ist eine Division mit 2b. Die große Frage ist nun, wofür wir überhaupt bitweise Operatoren benötigen?
Hierfür möchte ich zwei Beispiele angeben. Beginnen wir mit einem Beispiel, in dem wir Bitshift und das bitweise UND benötigen. Gehen wir mal davon aus, dass wir einen Farbcode erhalten haben
– sagen wir den Farbcode aus unserem Kapitel 4, nämlich 0xE9967A. Aus der hexadezimalen Schreibweise können wir den Rot- Grün-
und Blauanteil einfach ablesen. Rot ist 0xE9, Grün ist 0x96 und Blau ist 0x7A. Die zugehörigen Dezimalwerte wären 15308410 für den gesamten Farbcode und 233, 150 bzw. 122 für die RGB Werte.
Diese Werte möchten wir jetzt mit Hilfe eines Programms herausfinden – sagen wir für die Berechnung eines Grauwertes, bei dem R, G und B nach der Berechnung exakt der gleiche Wert ist und zwar
der Durchschnitt von den Farbwerten R, G und B. Wir können jetzt dem Rechner nicht ohne weiteres sagen „nehme vom Hexadezimalwert die rechten beiden Stellen“. Natürlich gäbe es solche Möglichkeiten
– wenn wir bspw. den Farbcode als Hexwert in einen String umwandeln und dann die rechten beiden Char Werte extrahieren. Das ist aber nicht der ideale Weg, da wir hier dem Rechner viel zu viele
unnötige Schritte aufbürden. Sehr viel eleganter geht dies mit bitweisen Operatoren. Sehen wir uns ein Unterprogramm an, welches diese Ermittlung für uns durchführt:
Listing 22: Usecase für Bitshift und bitweises UND/ODER
Kurze Erklärung der Codezeilen: Als Parameter erhalten wir die RGB Zahl. Mit einer Bitmaske
0xFF (also als Integer binär 0000 0000 0000 0000 0000 0000 1111 11112 verknüpfen wir die Zahl mit UND. Dies bedeutet, dass nur die letzten 8 Bit herauskommen. Nur hier haben wir die Möglichkeit,
dass wir 1 UND 1 = 1 erhalten (wenn eben in der
iRgb Zahl ein Bit die 1 hat – siehe
Abbildung 16). Danach schieben wir
iRgb um acht Stellen nach rechts und „schneiden“ wieder die rechten 8 Bits heraus. Das Ganze wird noch ein drittes mal gemacht. In den Variablen
b,
g und
r haben wir nun die Bits 1-8, 9-16 und 17-24 – allerdings rechtsbündig. Nun bilden wir den 8 Bit Durchschnittswert und geben alle Zahlen auf der Konsole aus. Danach wird in die Variable
grey der Durchschnittswert
avg auf die ersten 8 Bit gelegt, dann wird
avg um 8 Bit nach links verschoben und übernommen und nochmal um
16 Bit. Die Übernahme erfolgt mit ODER.
Hier nochmal das „Maskieren“ der rechten 8 Bit und der Rechtsshift als Grafik.
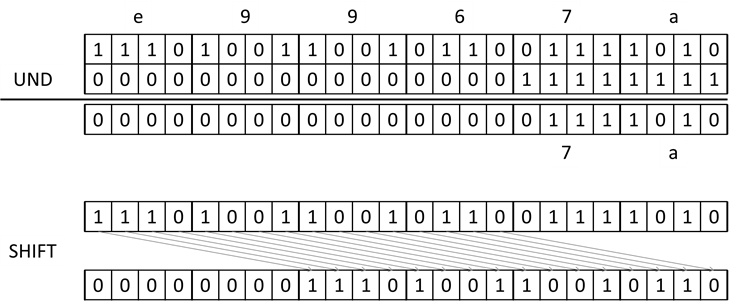
Abb.: 16: Maskieren der rechten 8 Bit und shift nach rechts
Ein weiterer häufig genutzter Fall für Bitshift und bitweiser UND/ODER Verarbeitung ist die Übergabe von logischen Flags an ein Unterprogramm. Wenn wir 1/0 (bzw. true/false) Zustände an ein Unterprogramm
übergeben wollen, so kann man dies entweder je Zustand über eine
boolean Variable durchführen oder wir definieren je eine Bitposition für einen Zustand. Solche „Schalter“ werden häufig bei komplexeren Elementen benötigt – bspw. in Java die Engine für die Verarbeitung
von regulären Ausdrücken, welche über 8 Flags erlaubt. Da wir in der Parameterliste nicht acht
boolean Variablen übergeben wollen, bietet sich hier die binäre Version an. Das folgende Programm soll uns nun einfach nur ausgeben, welche Bitposition der übergebenen
iFlags Variablen jeweils auf 1 gesetzt sind.
Listing 23: Flagübergabe als int Bits
Kurze Erklärung der Codezeilen: Das Unterprogramm
checkFlags() erwartet eine
int Variable als Parameter. Dort wird zuerst die Variable
„mask“ mit dem Wert 1 erzeugt. Hier ist also nur das rechte Bit auf 1 gesetzt. Nun wollen wir alle 32 Bits daraufhin prüfen, ob sie auf 1 gesetzt wurden. Deshalb benötigen wir eine entsprechende Schleife, welche alle
Bits durchläuft. Pro Durchlauf prüfen wir mit einem
„&“, ob in
iFlags das rechte Bit gesetzt ist. Wenn es gesetzt ist, wird das Ergebnis 0b1 sein. Wenn nicht 0b0. Vor dem nächsten Durchlauf schieben wir das Bit in
mask um eins nach links, weshalb dort nun 0b10 steht. Die
„&“ Verknüpfung kann somit nur die 0b10 für den Fall, dass das zweite Bit in iFlags gesetzt ist, oder 0b0 wenn nicht. Dies ist der Grund, warum in der Verzweigung auf „ungleich 0“ geprüft wird. Beim Aufruf initialisieren
wir die
iFlags Variable auf 0 – sprich alle Bits sind auf 0. Über ein ODER können wir nun einzelne Bits setzen, da 0 | 1 die 1 ergibt.
Die Ausgabe des Codes ist somit:
Nun müssen wir aber nochmal kurz auf eine Besonderheit des Bitshifts nach rechts eingehen. Sehen wir uns hierfür folgenden Code an:
Listing 24: Bitshift einer negativen Zahl
Die Ganzzahlige Division mit 23 müsste eigentlich -406 ergeben, bei uns kommt jedoch -407 heraus. Das liegt im Wesentlichen am Zweierkomplement, bei dem der
Überhang nicht abgeschnitten wird, sondern hinzugezählt wird. Sehen wir uns die Zahl als Bits an:

Abb.: 17: Arithmetischer Bitshift bei negativer Zahl
Soweit ist das Ergebnis übereinstimmend mit der Theorie. Trotzdem gibt es noch eine weitere Besonderheit, und zwar, dass das Ergebnis negativ ist. So merkwürdig sich das jetzt anhört – aber wenn wir uns die ersten,
durch die Verschiebung neu hinzugekommenen drei Bits ansehen, sind sie 1, nicht 0. Versuchen wir das gleiche Bitmuster wie bei -3254, jedoch tauschen wir das erste Bit von 1 auf 0, wodurch die Zahl 29514 herauskommt:
Listing 25: Bitshift einer positiven Zahl
Das Ergebnis ist nun 3689, was wir wiederum auf Bitebene nachvollziehen können:

Abb.: 18: Arithetischer Bitshift bei positiver Zahl
Hier wurden nun die ersten drei Stellen mit einer 0 aufgefüllt. Der Bitshift Operator nach rechts füllt also alle negativen Zahlen links mit 0 auf, alle positiven mit 1. Wollen wir aber einen
„echten“ Bitshift nach rechts – also einen der immer mit 0 auffüllt, müssen wir den Code mit dem dreifachen „>“ schreiben:
Listing 26: „echter“ Bitshift einer negativen Zahl
Das Ergebnis ist hier die 536870505, was folgendem Bitmuster entspricht:

Abb.: 19: Zerofill Bitshift bei negativer Zahl
Wir halten also fest, dass beim Bitshift nach rechts zwei verschiedene existieren. Derjenige, der das Vorzeichen erhält (weshalb man ihn auch als „arithmetischer Bitshift“ oder manchmal auch „sticky(6) Bitshift“ bezeichnet) und den
normalen, auch „zerofill Bitshift“ – also einer der mit 0 auffüllt. Bei manchen Programmiersprachen gibt es den „normalen“ jedoch nur für bestimmte Datentypen, meist
int.
(6) „Sticky“ – also klebend, da das Vorzeichenbit „kleben“ bleibt.
Der Vollständigkeit halber hier nochmal die wichtigsten Operatoren:
| Operation: | Notation: | C: | C++: | C#: | Java: | JavaScript: | PHP: | Python: |
|---|---|---|---|---|---|---|---|---|
| a UND b | a & b | X | X | X | X | X | X | X |
| a ODER b | a | b | X | X | X | X | X | X | X |
| a XOR b | a ^ b | X | X | X | X | X | X | X |
| a NICHT | ~a | X | X | X | X | X | X | X |
| Shift nach rechts um b Stellen (arithmetisch) | a >> b | X | X | X | X | X | X | X |
| Shift nach rechts um b Stellen (zerofill) | a >>> b | (7) | (7) | X | X | X | ||
| Shift nach links um b Stellen | a << b | X | X | X | X | X | X | X |
Tabelle 8: Bitweise Operatoren
(7) In C und C++ wird zerofill bei >> ausgeführt, wenn wir mit unsigned int arbeiten.

Operatoren für Speicherzugriff
Hatten wir bis hier noch beobachten können, dass die einzelnen Programmiersprachen sich sehr ähneln, wird dies bei den
Speicheroperatoren nicht mehr so sein. C (und somit auch C++) bieten hier als einzige einen durchgängigen Syntax für die
volle Kontrolle auf die Speicherinformationen. Lediglich PHP hat aufgrund der Unterstützung von expliziten call by reference
und call by value Aufrufen noch einige wenige Ausnahmen. Aus diesem Grund werde ich mich bei den folgenden Erklärungen auf die
Programmiersprache C konzentrieren. Unser Speichermodell soll nun zum einen eine
int Variable
i mit einem Wert 99 belegen, die Adresse von
i in eine Pointervariable
j übernehmen und dann über die Pointervariable
j auf den Wert 99 zugreifen. Zum anderen soll ein
struct mit zwei
int Variablen
x und
y definiert werden. Die Variable
p soll nun einen Zeiger auf dieses
struct namens
„coords“ erhalten und dann sollen die Werte 10 bzw. 20 zugewiesen werden:
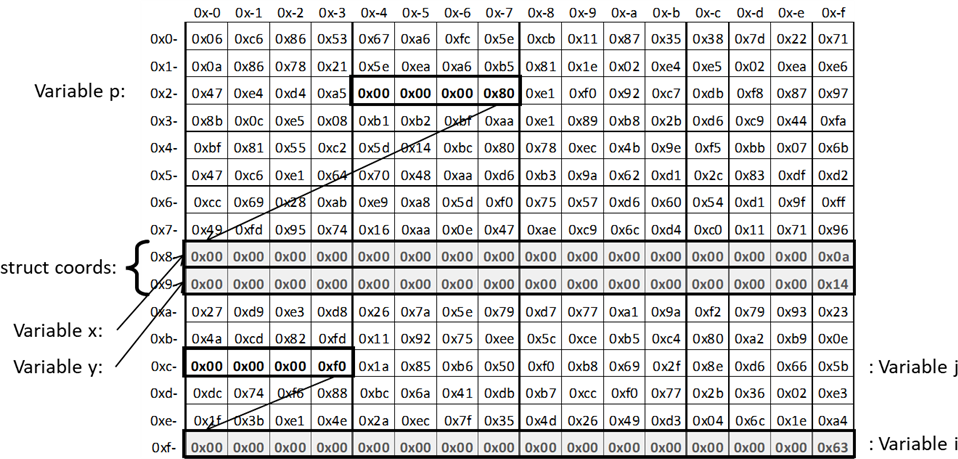
Abb.: 20: Speichermodell für die Zugriff- und Speicheroperatoren
Der zugehörige C Code setzt diese Forderung nun um:
Listing 27: Beispielcode für die Nutzung der Speicheroperatoren
Wir sehen uns hier jetzt nur die Zugriffe auf die Variablen und Pointer an – nicht die Deklarationen und
Speicherreservierungen. Beginnen wir mit der Zuweisung
j = &i;. Hier übernehmen wir die Adresse von
i in die Variable
j. Der
& Operator ermittelt in diesem Zusammenhang die Adresse von
i. Beim Zugriff auf
„j“ können wir nun über den
* Operator nun auf den Inhalt zeigen, auf den
j zeigt. Dies wird „Dereferenzierung“ genannt, da wir nicht mehr mit der Referenz, sondern mit dem Wert arbeiten.
Bei der Nutzung des
struct erzeugen wir zuerst eine Zeigervariable auf dieses
struct, für das wir nun einen Speicher reservieren müssen. Beim eigentlichen Zugriff habe ich nun beide Möglichkeiten
dargestellt. Der Ausdruck
*p dereferenziert wieder
p, so dass wir auf das eigentliche
struct zugreifen können. Mit dem Punktoperator greifen wir somit auf internen Elemente eines
struct (bzw. in objektorientierten Sprachen auch eines Objektes) zu. Die Klammer um
*p ist hier notwendig, da wir nicht auf ein Element von
p zugreifen können (in
p ist ja nur die Adresse), sondern auf das Objekt, auf das
p zeigt. Da in C (und C++) häufig mit Pointern auf Objekte gearbeitet wird und der Ausdruck mit Dereferenzierung, Klammer
und Punktoperator relativ umständlich zu schreiben ist, hat man den Elementzugriffsoperator
-> eingeführt. Wie wir im Code sehen, sind diese beiden Versionen
(*p).x und
p->x austauschbar.
Insofern haben wir die wichtigsten Operatoren für die Speicherzugriffe kennengelernt:
| Operation: | Funktion: | Notation: | C: | C++: | C#: | Java: | JavaScript: | PHP:(8) | Python: |
|---|---|---|---|---|---|---|---|---|---|
| Adressermittlung | Ermittelt Adresse von a | &a | X | X | X | ||||
| Dereferenzierung | Greift auf Daten zu, auf die b zeigt | *b | X | X | |||||
| Elementzugriff | Greift auf Element x von a zu | a.x | X | X | |||||
| Elementzugriff Zeiger | Greift auf Element x des Konstrukts zu, auf das b zeigt | b->a | X | X |
Tabelle 9: Operatoren für Speicherzugriff
(8) Bei PHP handelt es sich um „Referenzen“, keine Adressen!

Sonstige Operatoren
Kommen wir nun zu den Operatoren, welche ich als „den Rest“ bezeichnen möchte. Die meisten dieser Operatoren haben wir in den
vorausgegangenen Kapiteln entweder schon kennengelernt oder sie sind selbsterklärend. Beginnen wir mit den bereits bekannten
Operatoren. Den Typecast haben wir mit den runden Klammern bereits in
Kapitel 6 besprochen. Wir setzen den Zieldatentyp in Klammern vor den Wert,
was den Datentyp für die aktuelle Nutzung des Wertes kurzzeitig umwandelt. Die runden Klammern haben aber noch eine weitere
Bedeutung außerhalb des Typecasts. Genau wie in der Mathematik können wir mit Hilfe von runden Klammern die Priorisierung
von Abarbeitungen steuern. Klammerausdrücke werden immer priorisiert behandelt und der Prozessor geht hier immer von innen
nach außen vor – eben genauso wie in der Mathematik.
Ein weiterer bekannter Operator ist die Indizierung, welche wir vor allem für Arrays benötigen. Die Indexposition wird einfach
in eckigen Klammern angegeben und der Prozessor weiß somit, auf welches Element im Array er zugreifen muss. Bei den
mathematischen Operatoren fehlt uns noch die Negation in den negativen Zahlenbereich – was wieder aus der Mathematik entlehnt
wurde. Es wird einfach das Minuszeichen vor den Operanden geschrieben, wodurch dieser zahlenmäßig negiert wird.
Soweit zu den bekannten bzw. offensichtlichen Operatoren Kommen wir nun zu den zwei weniger offensichtlichen, welche jedoch
an manchen Stellen das Programmieren durchaus vereinfachen können. Beginnen wir mit einen der wenigen ternären Operatoren,
weshalb er oft auch einfach nur als „der ternäre Operator“ bezeichnet wird – der Bedingungsoperator. Manche kennen ihn auch
unter dem scherzhaften Namen „Elvis Operator“, da die beiden notwendigen Symbole, das ? und der : zusammengeschrieben und um
90° gedreht wie die Haare von Elvis Presley über seinen Augen aussehen
 Hier ein Beispiel in JavaScript:
Hier ein Beispiel in JavaScript:
 Hier ein Beispiel in JavaScript:
Hier ein Beispiel in JavaScript:
Listing 28: Bedingungsoperator in JavaScript
Der Bedingungsoperator erwartet vor dem
? einen
boolean Wert. Wenn dieser
true ist, wird der Code vor dem
: ausgeführt, ansonsten der Code nach dem
:. Dieser Operator wird gerne genommen, wenn man sehr kompakten Code erzeugen möchte. Es ist aber relativ einfach mit einer
Verzweigung zu ersetzen.
Der zweite „neue“ Operator ist der Kommaoperator. Die Idee hinter diesem Operator ist, dass der Prozessor eigentlich einen
Ausdruck erwartet, trotzdem mehrere eingetragen werden dürfen. Wenn eine Zuweisung erwartet wird, so werden zwar alle mit
Komma getrennten Ausdrücke abgearbeitet, jedoch nur der letzte wird verwendet. Meist wird er aber für die Abarbeitung von
Code – bspw. mehrerer Deklarationen oder Manipulationen verwendet. Hier ein Beispiel:
Listing 29: Kommaoperatorn in JavaScript
Wenn wir den Code ausführen, sehen wir:
Es wurden also beide Deklarationen, eine für
i und eine für
j ausgeführt und ganz rechts beide Manipulationen, die
i++ und
j--, obwohl im vorderen und hinteren Bereich der Zählschleifensteuerung nur ein Ausdruck erwartet wird. In der Mitte sind
zwei Bedingungen, von denen aber nur die letzte relevant ist, da wir ja in der Ergebnismenge für
i auch Werte größer gleich 2 finden aber keine kleiner für
j kleiner gleich 1.
| Operation: | Funktion: | Notation: | C: | C++: | C#: | Java: | JavaScript: | PHP: | Python: |
|---|---|---|---|---|---|---|---|---|---|
| Typecast | Temporäre Typumwandlung nach typ | (typ)a | X | X | X | X | X(9) | X | X(9) |
| Priorisierung | Abarbeitung von innen nach außen | a*(b+c) | X | X | X | X | X | X | X |
| Indizierung | Zugriff auf n. Element eines Arrays | a[n] | X | X | X | X | X | X | X |
| Negation | Negation des Zahlenwertes a | -a | X | X | X | X | X | X | X |
| Bedingung | Wenn b = true, dann verarbeitung c, sonst d | b?c:d | X | X | X | X | X | X | X(10) |
| Komma | Verarbeitung von a, b, c und ggf. Übernahme von c | a, b, c | X | X | X | X | X | X | X |
Tabelle 10: Sonstige Operatoren
(9) Nur mit eigenen Methoden, nicht über () Operator.
(9) Syntax in Python: c if b else d
(9) Syntax in Python: c if b else d

CC Lizenz (BY NC SA)
