Ein erster Schritt in die Programmierwelt
Wir haben ja schon festgestellt, dass unser Computer recht genaue Anweisungen benötigt, um das zu tun was wir von ihm
wollen. Der Algorithmus für die Überquerung der Straße war hierfür ein Beispiel. Was ist aber ein Algorithmus eigentlich
und wie unterscheidet er sich von einem Programm? Hierzu überlegen wir uns mal eine kleine Aufgabe, die unser Computer
für uns realisieren muss – er soll nämlich Zahlen raten lassen. Der Computer „überlegt“ sich eine zufällige Zahl zwischen
0 und 1000 und wir als User müssen sie erraten. Der Computer sagt uns dabei, ob die von uns geratene Zahl größer oder
kleiner der zu erratenden Zahl ist. Das ist zugegebenermaßen nicht das spannendste Spiel, aber es hilft uns ein paar
grundlegende Gedanken zu fassen.
Wir kommen hier beispielsweise schon zum ersten Problem von uns Menschen – wir neigen
zur Ungenauigkeit. Wir haben mit der Aussage „zwischen 0 und 1000“ nicht exakt vorgegeben, ob die 0 bzw. die 1000 eine
mögliche Zahl ist (also „inklusive“) oder nicht, weil der Begriff „zwischen“ nicht genau definiert ist. Zwei Beispiele:
Ich sage zu meinem Kollegen „ich werde zwischen 12:00 und 15:00 vorbeikommen“. Wenn ich um genau 15:00 vorbei komme, wird
er sich nicht beschweren können, da ich ja noch pünktlich war. Hier bedeutet „zwischen“ also inklusive der angegebenen
Grenzen. Anders verhält es sich mit Abständen. Wenn ich beispielsweise mit einem sehr großen Auto durch ein sehr kleines
Tor fahren möchte, so muss es zwischen die beiden Torpfosten passen. Die Außenspiegel müssen also kleiner als das Maß
zwischen den Pfosten sein (und für die ganz „Genauen“ unter uns – auch wenn es auf den Nanometer gleich wäre, eine Bewegung
wäre dann auch nicht möglich). Hier bedeutet „zwischen“ also exklusive der angegebenen Grenzen. Wir müssen uns also
unserer Ungenauigkeit bewusst werden, damit wir exakt formulieren können was wir eigentlich wollen. Nur dann ist es
möglich, den Computer genau dazu zu bringen, auch das zu tun was wir wollen. In unserem Beispiel sagen wir einfach,
dass die beiden Zahlen 0 und 1000 mögliche zu ratende Zahlen sind, also „inklusive“ der Grenzen.
Diese Aufgabe ist nun nicht sehr komplex aber immerhin erfüllt sie die wesentlichen Merkmale eines Algorithmus. Nun,
wie soll der Rechner das Ganze nun machen? Zuerst soll er die Zufallszahl erzeugen. Danach muss der User die Möglichkeit
haben, eine Zahl einzugeben, welche wiederum vom Computer analysiert wird. Hier gibt es drei Situationen – die Zahl ist
zu groß, zu klein oder die Zahl wurde erraten. Der Computer muss dann schließlich die Info an den User weitergeben. Im
Fall, dass der User die Zahl nicht errät, soll er wieder eine neue Zahl eingeben können. Errät er die Zahl, endet das
Programm.
Die Frage ist nun, kann man so ein Vorgehen etwas griffiger formulieren? Es wäre beispielsweise möglich, eine Art
„Befehlsform“ zu verwenden, in der die durchzuführenden Schritte beschrieben werden. Eine Idee wäre folgende Form:
Das ist zwar schon etwas übersichtlicher, aber immer noch nicht wirklich zufriedenstellend. Es fehlt eine gewisse
Stringenz bei der Formulierung, so dass uns die Orientierung in den Anweisungen schwerfällt. Eine bessere Möglichkeit
wäre beispielsweise eine Art „Flussdiagramm“ – oder auch Programm Ablauf Plan (kurz: PAP).

Programm Ablauf Plan (PAP)
Im Programm Ablauf Plan (kurz: PAP) gibt es im Wesentlichen vier wichtige Elemente:
| Symbol: | Bedeutung: |
|---|---|
 |
Flusslinie. Diese zeigt die Verarbeitungsrichtung an. |
 |
Terminator. Dieser steht am Anfang (Beschriftung „Start“) oder am Ende (Beschriftung „Stopp“) und markiert den Start oder das Ende des Algorithmus. |
 |
Aktionen stellen eine Operation dar, welche der Computer durchführen soll. Hierunter fallen auch Eingabeaufforderungen oder Ausgaben (1). |
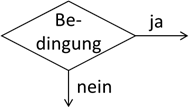 |
Verzweigung. Hier entscheidet man basierend auf einer Bedingung, die entweder mit „ja“ oder „nein“ beantwortet werden kann, welcher Zweig abgearbeitet werden soll. |
Tabelle 1: Symbole des PAP Diagramms
(1) Man sieht mitunter für Eingabeaufforderungen und Ausgaben ein eigenes Symbol in Form eines Parallelogramms
Unser kleiner Algorithmus würde nach dieser Notation nun wie in Abbildung 1 aussehen.
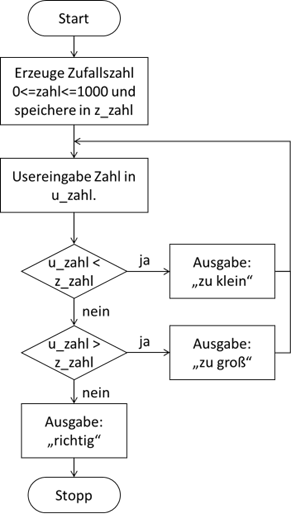
Abb.: 1: Algorithmus "Zahlenraten"
Hier fällt nun vorab schon mal folgendes auf:
- Gleiche funktionale Blöcke werden gleich gezeichnet.
- Es ist sehr viel einfacher, die Logik des Ablaufes nachzuvollziehen.
- Die zu erratende Zahl und die vom User geratene Zahl haben mit „z_zahl“ und „u_zahl“ einen eindeutigen Namen erhalten, so dass wir sie leicht unterscheiden können.
- Die Verzweigungen sind hintereinander platziert, so dass die beiden „nein“ Zweige eine eigene Prüfung auf „richtig geraten“ (also u_zahl ist gleich z_zahl) überflüssig machen.
- Durch die Rückführung der beiden „ja“ Zweige nach Oben erhalten wir die Wiederholung eines Teils des Algorithmus – was wir auch als „Schleife“ bezeichnen.
Diese Notation ist zwar schon mal eine erhebliche Verbesserung im Vergleich zu unserer Wortbeschreibung des Algorithmus,
allerdings ist dies immer noch nicht die „hohe Schule“ der Notation. Der Grund liegt in der Möglichkeit, beliebig Pfeile
nach Oben oder Unten zu ziehen. Diese „Flexibilität“ bezüglich der Pfeilnutzung führt oftmals zu wilden Graphen, welche
am Ende nicht mehr sauber umsetzbar sind. Wir werden später eine weitere Notation kennenlernen , welches im Regelfall zu
saubererem Code führt (2). Doch alles zu seiner Zeit.
(2) Das Nassi-Shneidermann Diagramm oder auch „Struktogramm“ wird in einem späteren Kapitel besprochen

Algorithmus
Was wir nun geschaffen haben, ist ein „Algorithmus“. Hierin haben wir jetzt sauber beschrieben, wie unser „Problem“ zu
lösen ist – wir sind nun also in der Lage, einem „dummen System“ wie dem Computer unser Anliegen haarklein zu erklären.
Wir haben aber immer noch nicht geklärt, was exakt nun ein Algorithmus ist – und wie er sich beispielsweise von einem
Programm unterscheidet. Von der Idee her ist ein Algorithmus eine sinnvolle Abfolge von Anweisungen, welche ein
gegebenes Problem lösen. Die Anweisungen müssen jedoch nicht in einer bestimmten Programmiersprache ausgeführt werden –
es reicht eine strukturierte Erklärung in Form von frei formulierten Anweisungen. Hierbei müssen die einzelnen
Anweisungen aber gewisse Eigenschaften aufweisen:
Ausführbarkeit: So merkwürdig es klingt, die einzelnen Schritte müssen ausführbar sein. Diese „Einschränkung“
ist notwendig, weil man eben nicht auf eine Programmiersprache pocht, welche die Ausführbarkeit ja per Definition
bereits eingebaut hat. Niemand würde auf die Idee kommen, eine Programmiersprache zu entwickeln, die nicht ausführbar
ist. Wenn wir beispielsweise den Spieß umdrehen und der Computer müsste eine von uns erdachte Zahl raten, wäre die
Anweisung „Computer errät Zahl“ nicht ausführbar.
Eindeutigkeit: Dies hängt eng mit der Ausführbarkeit zusammen. Die Forderungen dürfen sich nicht widersprechen
und sie dürfen keinen Raum für Interpretationen lassen. Dies war beispielsweise bei der ursprünglichen Anforderung
„zwischen 0 und 1000“ nicht ganz erfüllt.
Terminiertheit: Der Algorithmus muss nach einer endlichen Anzahl von Verarbeitungsschritten zu einem definierten
Ende kommen und ein Ergebnis im Sinne einer gelösten Problemstellung liefern.
Determiniertheit: Wenn der Algorithmus unter den gleichen Eingangsbedingungen öfter läuft, muss immer das
gleiche Ergebnis geliefert werden. Er darf also keine „Zufallsergebnisse“ liefern (wobei hier das Ergebnis der
Problemlösung gemeint ist). Streng genommen ist auch die „Zufallszahl“, welche vom Rechner erzeugt wird keine wirkliche
Zufallszahl, sondern ein determinierter Algorithmus, der das Zufallselement einfach aus dem Zeitpunkt generiert, wann
die Zufallszahl erzeugt wird.
Determinismus: Hierunter versteht man, dass nach jedem Schritt ein eindeutig definierter Folgeschritt existiert
(mit Ausnahme es Endzustandes). Dies ist eine Grundvoraussetzung, damit der Algorithmus eindeutig und determiniert ist.
Endlichkeit: Diese Eigenschaft ist eher akademischer Natur – sie fordert, dass die Formulierung des Algorithmus
nicht unendlich lang sein darf.
Der Algorithmus beschreibt also eher die Lösungsstrategie als die tatsächliche Implementierung. Wenn ich nun basierend
auf dem Algorithmus eine Software realisiere, dann haben wir ein Programm erstellt. Pro-gramme sind also in einer
bestimmten Programmiersprache umgesetzte Algorithmen.

Implementierung HTML
Jetzt haben wir uns schon die Arbeit gemacht einen Algorithmus zu definieren – dann wollen wir das Ganze auch als
Programm realisieren. Damit wir für den Anfang nicht zu viel an Entwicklungstools installieren müssen, werden wir unser
kleines Programm in JavaScript realisieren. Aber erstmal der Reihe nach. Warum ist es so einfach in JavaScript zu
entwickeln? Nun, wir werden uns zwar erst in einem späteren Kapitel mit den Unterschieden zwischen Skript- und kompilierten
Sprachen auseinandersetzen. Ein paar einleitende Infos können aber an dieser Stelle nicht schaden.
JavaScript wurde entwickelt, um Webseiten dynamisch zu machen. Immer, wenn wir eine Seite im Internetbrowser öffnen,
bei denen wir Daten eingeben und Ergebnisse auf der gleichen Seite zurückbekommen, ist JavaScript im Spiel. Das heißt,
JavaScript wird von jedem Webbrowser verarbeitet – wir brauchen also keine weiteren Tools, da ja fast jeder Rechner
einen Webbrowser installiert hat. Weiterhin können wir mit unseren Browsern nicht nur Webseiten von irgendwelchen
Servern ansehen, sondern auch lokal gespeicherte Dokumente, sogenannte „HTML“(3) Dokumente öffnen. In diesen HTML
Dokumenten wiederum können wir JavaScript Code einbetten. Mit anderen Worten, wir können ein solches File selbst
erstellen, auf unserer Festplatte speichern und dann mit einem Browser öffnen – wir haben also alles was wir zum
Programmieren brauchen.
(3) HTML steht für Hypertext Markup Language und ist eine Auszeichnungssprache für das WWW
Unsere Webseite benötigt nun ein paar Interaktionselemente, damit wir als User damit umgehen können. Im Wesentlichen
handelt es sich um ein Eingabefeld für die vom User geratene Zahl und ein Button, welcher die Verarbeitung triggert.
Noch besser für das Handling wäre die Verarbeitung nach Betätigung der Enter Taste, aber wir wollen es für den Anfang
nicht zu kompliziert machen. Weiterhin muss der Computer in der Lage sein, das Ergebnis irgendwo sichtbar zu machen,
sprich wir brauchen ein Ausgabefeld. Sammeln wir mal unsere Elemente und vergeben gleich einen eindeutigen Namen:
| Was: | Name: | Bedeutung: |
|---|---|---|
| Eingabefeld | numbInput | User gibt Zahlen ein |
| Button | playButton | Bei Anklicken wird die eingegebene Zahl als u_zahl verarbeitet, indem die Funktion myButtonClicked aufgerufen wird. |
| Textfeld | gameOutput | Die „zu groß“, „zu klein“ und „richtig“ Information wird nach der Verarbeitung ausgegeben. |
Tabelle 2: Funktionsdefinition unseres Programms
Damit haben wir die Funktionalitäten der einzelnen Elemente festgelegt. Diese decken sich auch mit der Algorithmus
Beschreibung, womit wir den Algorithmus nahtlos in unser Programm einbauen können. Was nun noch bei den vorbereitenden
Maßnahmen fehlt, ist das Design unserer kleinen Webseite. Hierzu zeichnen wir grob das Layout, damit wir ein Gefühl
dafür bekommen, wie wir die HTML Datei aufbauen müssen:
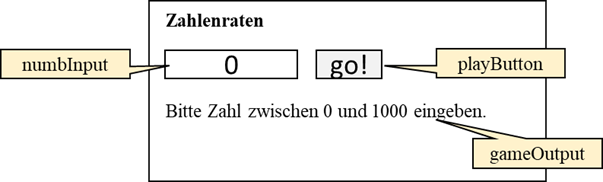
Abb.: 2: Layout Webseite "Zahlenraten"
Damit der Bereich für die Textausgabe am Anfang nicht leer ist, geben wir einfach eine kurze Anweisung für den User an,
welche danach durch die Ergebnisse ersetzt wird. Die Namen der Elemente gebe ich hier an, damit der Link zwischen unserer
Tabelle 2 und dem Layout eindeutig ist.
Nun können wir unsere HTML Seite erstellen. Hierzu erzeugen wir auf unserem Rechner eine Datei, namens
MeinZahlenraetsel.html. Wichtig ist, dass wir tatsächlich die Dateierweiterung
„.html“ haben, damit wir die Datei mit unserem Browser öffnen können.
Hinweis: Wer die Dateierweiterung unter Windows nicht ändern kann, klickt im Fileexplorer den Haken im Menü „Ansicht“
bei „Dateinamenerweiterungen“ an. Danach werden sie angezeigt und können auch geändert werden.
Die HMTL Implementierung unseres kleinen Projektes müssen wir jetzt nicht vollständig verstehen – dieses Buch
beschäftigt sich primär mit der Programmierung, nicht mit HTML. Wer trotzdem sich die Details näher ansehen will, dem
seien Webseiten wie
www.selfhtml.org
oder
www.w3schools.com
empfohlen. Die für unser Programm wichtigen Elemente werde ich hier aber trotzdem kurz erläutern. Die Anfangsstruktur
unseres HTML Files soll nun wie folgt aussehen:
Listing 1: HTML Seite ohne Funktion
Alle für die HTML Interpretation relevanten Informationen stehen zwischen den beiden „Tags“
<html>
und
</html>
. Die anzuzeigenden Informationen stehen dann zwischen den beiden
<body>
Tags. Zwischen den <head> Tags wiederum stehen allgemeine und zentrale Informationen, wie z.B.
auch der JavaScript(4) Code. Wir finden in unserem Header zwei JavaScript Funktionen. Eine, welche
beim Laden der Seite
(initProgram())
und eine, welche beim Klick des Buttons
(myButtonclicked())
aufgerufen wird, wodurch wir die Eingabe abschließen werden. Die Initialisierung wird dadurch
unser „Start“ Element des Algorithmus in PAP Notation von Abbildung 1.
(4) In größeren Projekten wird der JavaScript Code in der Regel in eigene Files ausgelagert.

Implementierung JavaScript
So viel zu HTML. Nun können wir uns ganz dem Code widmen. Beginnen wir mit den „Variablen“. Variablen sind eine
Art Speicher, in denen wir Informationen ablegen können. Wir werden uns die Hintergründe dieser Variablen
in einem späteren Kapitel genauer ansehen. Für jetzt sind es lediglich Speicher. Nachdem die Speicher von allen
benötigt werden, machen wir sie „global“, was so viel heißt, wir schreiben sie einfach außerhalb der Funktionen hin,
wodurch sie von überall zugreifbar sind.
„var“
steht hier für Variable(5), danach kommt der Variablenname und die initiale Zuweisung mit einem definierten Wert – in
unserem Fall die 0. Wir Ergänzen unser HTML File also wie folgt:
(5) Details zur Variablendeklaration in JavaScript (und wie man es besser macht) finden sich in einem späteren Kapitel.
Listing 2: Globale JavaScript Variablen
Damit haben wir die beiden Variablen
z_zahl
und
u_zahl erzeugt und wir können in unserem gesamten JavaScript Programm darauf zugreifen – sprich sie mit neuen Werten
belegen bzw. die existierenden Werte auslesen. Nun wollen wir aber, dass bei Programmstart ein Zufallswert zwischen
0 und 1000 gesetzt wird. Genau hierfür haben wir unsere Funktion
initProgram()
vorgesehen:
Listing 3: Initialisierung des Programms
In
initProgram()
setzen wir also die Startwerte gleich für unsere beiden Variablen.
z_zahl
wird mit einer Zufallszahl belegt.
Kurze Erklärung der Codezeilen:
Math.random() erzeugt eine (pseudo-) zufällige Gleitkommazahl zwi-schen = 0 und < 1 – sagen wir mal
0,13808586331415706. Dann wird sie mit 1001 multipliziert. Das Ergebnis ist somit 138,22394917747121706.
Math.floor()
wiederum schneidet alle Nachkommastellen ab, wodurch 138 übrigbleibt. Jetzt mag der ein oder andere fragen,
warum ausgerechnet mit 1001 multipliziert wird und nicht mit 1000. Gehen wir es einfach mal durch. Wenn unser
Math.random()
die kleinstmögliche Zahl ausspuckt – die 0 – dann wird 1001 mit 0 multipliziert und das Ergebnis wäre die 0, was
auch unsere kleinste zu erwartende Ratezahl wäre. Wenn allerdings
Math.random() die größtmögliche Zahl ausgibt, was ja < 1 war, so wäre es die 0,99999999999999999.
Multiplizieren wir dies mit 1001, so erhalten wir die 1000,99999999999999999, was wiederum durch
Math.floor() zu 1000 umgewandelt wird.
u_zahl
entnehmen wir gleich dem Texteingabefeld, da wir über den HTML Code ja mit
value="0"
einen Initialwert in das Feld gesetzt haben und der dem User angezeigte und in
u_zahl
gespeicherte Wert immer synchron sein müssen.
Kurze Erklärung der Codezeilen:
document.getElementById("numbInput").value
sucht in der HTML Seite ein Element mit der ID
„numbInput“. Wir haben ein Element mit dieser ID vorgesehen, also wird es auch gefunden. Der Typ dieses Elements ist
ein HTML Input Element und hat somit eine
„value“ Eigenschaft. Diese lesen wir mit diesem Befehl aus und schreiben den Wert mit dem Istgleichzeichen in die
Variable
u_zahl.
Soweit alles einleuchtend. Nun wollen wir mit Hilfe des Button-Klicks in die Verarbeitung gehen. Hierfür haben wir
die Funktion
myButtonclicked()
vorgesehen. Die Verarbeitung muss jetzt aus zwei Bereichen bestehen. Erstmal die Übernahme der eingegebenen Zahl in
unsere Variable
u_zahl.
Dann erfolgt die Auswertung entsprechend des Algorithmus. Es ist immer eine gute Idee, den Code übersichtlich zu
gestalten, weshalb wir diese beiden Funktionalitäten auch in eigenen Unterprogrammen realisieren wollen. Ich nenne
die Unterprogramme jeweils
getNumber()
und
processInput(). Damit ist die einzige Aufgabe des Unterprogramms
myButtonclicked()
im Prinzip der Aufruf dieser beiden neuen Unterprogramme:
Listing 4: Verarbeitung des Button Klicks
Sehen wir uns nun
getNumber()
an, welche nicht nur die Zahl übernimmt, sondern auch noch einen „Wahr“ (engl. „true“) bzw. „Falsch“ (engl. „false“)
Wert zurückgibt, damit wir sie in eine If-Abfrage einbauen können. Hier müssen wir nämlich zwei Probleme lösen.
Erstens müssen wir die Zahl aus der HTML Seite lesen. Dies haben wir in
initProgram()
ja bereits gesehen. Allerdings kann jetzt jeder beliebige Wert in dem Feld stehen, da der User ja die Eingabe gemacht
hat und wir nicht dafür garantieren können, dass er alles richtig macht. Dies führt uns zum Problem des
„Errohandlings“. Beim Programmieren gehen wir immer von einem User aus, der sagen wir mal nicht sehr intensiv
nachdenkt und alle möglichen Fehler macht. Der Programmierer spricht hier scherzhaft vom „dümmsten anzunehmenden User“,
kurz „DAU“. Unser gedachter User macht also alles falsch, was man falsch machen kann. Insofern würde er nicht nur
Zahlen eingeben, sondern auch Text, den wir natürlich nicht sinnvoll verarbeiten könnten. Also müssen wir zuerst prüfen,
ob er eine Zahl eingegeben hat. Wenn nicht, dann nehmen wir die letzte bekannte Zahl und schreiben sie wieder in das
Eingabefeld hinein und geben ein
„false“ zurück, ansonsten übernehmen wir die Zahl und melden ein
„true“:
Listing 5: Übernahme der eingegebenen Zahl plus Fehlerbehandlung
Was wir nun gemacht haben ist, unseren Algorithmus zu erweitern. Diese Fehlerbehandlung war ja nicht Teil
unseres ursprünglichen Ansatzes. Hier sehen wir ein oft auftretendes Problem beim Softwaredesign. Oftmals
erkennen wir erst beim Programmieren, wo noch offene Flanken des Algorithmus sind. Der Designer des Algorithmus
konzentriert sich auf das eigentliche Problem – sprich ein Spiel zum Zahlenraten zu erstellen. Hierbei
fokussiert er sich oftmals nicht auf die flankierenden Probleme, wie die der Fehleingaben. Streng genommen hat
er es zwar „angesprochen“, indem er die Forderung „Usereingabe Zahl in u_zahl“ formuliert hat (er verlangt also
explizit eine „Zahl“). Er hat aber nicht definiert, was bei Fehleingaben zu tun ist. Diese Problematik führt
bei realen Programmierprojekten oftmals zu unnötigen Verzögerungen. Gehen wir davon aus, der Programmierer
richtet sich zu 100% nach den Angaben im PAP – er setzt also kein vollständiges Errorhandling um. Danach wird
getestet und ganz am Ende kommt heraus, dass das Errorhandling nicht ausreichend ist. Nun wird der Algorithmus
erweitert und dann geht der Entwicklungs- und Testprozess von vorne los, was bei großen Projekten zu unschönen
Verzögerungen führen kann. Um diese Problematik zu entschärfen hat man agile Prozesse definiert, bei denen das
iterative Vorgehen zum Standard erhoben wird und der Entwickler sich in möglichst kurzen Abständen mit den
Designern abstimmt. Gehen wir nun aber noch kurz durch den Code durch:
Kurze Erklärung der Codezeilen: Zuerst übernehmen wir den eingegebenen Wert in eine neue Variable
inputVal, damit wir sie später einfacher weiterverarbeiten können. Das danach folgende
if ist eine sogenannte „Verzweigung“. Wir haben solche eine Verzweigung ja bereits in unserem Algorithmus kennen
gelernt. Wenn eine Bedingung erfüllt ist, mache das eine, ansonsten überspringe es. Die Bedingung ist ein
sogenannter Regulärer Ausdruck, mit dessen Hilfe wir prüfen können, ob der String nur aus Ziffern besteht
(engl. „digits“ – also
„\d“ und zwar ein bis mehrere, wofür das
„+“ steht, bis zum Ende des Ausdrucks
„$“):
(/\d+$/.test(inputVal) ergibt also
true, wenn
inputVal eine Zahl enthält). Wenn dem so ist, übernehmen wir den eingegebenen Wert in die Variable
u_zahl und beenden das Unterprogramm, indem wir
true zurückgeben. Wenn nein, dann schreiben wir den aktuellen Wert aus
u_zahl in die Eingabemaske, damit die fehlerhafte Eingabe mit dem alten Wert überschrieben wird und geben
false zurück.
Somit haben wir also in der Variable
u_zahl den aktuell eingegebenen Wert. Wenn nun die Funktion
myButtonclicked() das Unterprogramm
getNumber() aufgerufen hat und dieses fertig abgearbeitet wurde, springt der Computer wieder in
myButtonclicked() zurück und es erfolgt dort die Auswertung der Verzweigung – sprich hat der User eine gültige
Zahl eingegeben, welche ja zum Rückgabwert „Wahr“ geführt hat. Wenn dem so ist, wird der Aufruf des nächsten
Befehls ausgeführt, nämlich
processInput():
Listing 6: Verarbeitung der Daten
Das ist nun der eigentliche Kern des Algorithmus. Es ist durchaus bemerkenswert, dass der „Overhead“ eines Programms
für die Realisierung eines Algorithmus relativ groß ist. Grundsätzlich leuchten die Schritte zwar ein, aber es ist
nicht wirklich befriedigend, wenn man so viel zusätzlichen Code schreiben muss, nur um den eigentlichen Kern zu
realisieren. Da dieser Overhead aber oftmals standardisiert ist, gibt es eine Vielzahl von Hilfsprogrammen, welche
dem Entwickler hier unter die Arme greifen. Diese versuchen möglichst viel von diesen Overheadarbeiten automatisch
zu generieren und den gesamten Entwicklungsprozess, wenn möglich automatisieren. Solche Hilfsprogramme nennt man
„Integrated Development Environments“, kurz „IDE".
Kurze Erklärung der Codezeilen: Die eigentliche Verarbeitung erfolgt durch zwei Verzweigungen, wie wir es auch im
PAP hinterlegt haben. Die Abfragen können 1:1 übernommen werden. Das Setzen des Ausgabetextes wird wieder über
„document.getElementById()“ realisiert, diesmal wird aber das Element
„gameOutput“ gesucht. Da das Suchen aber über einen relativ langen Ausdruck erfolgt, können wir diese
Teilfunktionalität auch in einem eigenen Unterprogramm realisieren und es wiederverwenden. Wir sehen auch, dass die
Funktion
setInfoText(newInfoText) zwischen den Klammern noch einen Parameter aufweist. Dieser ist zu sehen wie eine Variable,
welche durch den Aufruf gesetzt wird. Der Aufruf
setInfoText("zu klein") führt also dazu, dass der Wert "zu klein" in die Variable
newInfoText geschrieben wird.
Somit ist unser gesamter Code fertig und wir können das Programm ausführen. Zur Kontrolle habe ich das gesamte
Listing nochmals in
GitHub
online gestellt. Wenn wir mit einem Doppelklick das File öffnen, startet der voreingestellte Webbrowser und wir
sehen unseren Anfangstext. Bei Eingabe einer Zahl und dem Klick auf „go!“ erhalten wir dann das Ergebnis der
Auswertung im unteren Bereich.
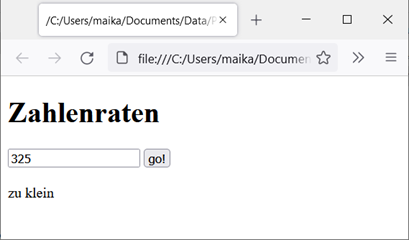
Abb.: 3: Abbildung 3: Screenshot HTML Zahlenraten
Was dem ein oder anderen vielleicht jetzt auffällt ist, dass wir das ganze Programm nur einmal durchlaufen können.
Wenn wir nochmals spielen wollen, müssen wir die Seite neu laden. Dadurch wird die
initProgram() Funktion nochmals aufgerufen und es beginnt von neuem. Durch eine einfache Erweiterung können wir dieses
eher umständliche Vorgehen vereinfachen. Wir ergänzen einfach einen neuen Button, bspw. mit der Aufschrift „Start“, und
lassen durch diesen Button die Funktion
initProgram() nochmals aufrufen. Wer möchte, kann diesen Button selbstständig ergänzen. Die wichtige Erkenntnis hierbei ist,
dass wir durch die Modularisierung unseres Codes in einzelnen Unterprogramme eine gewisse Flexibilität erreichen, welche
Anpassungen im Programm sehr stark erleichtern.
Nun, was nehmen wir als Programmierneulinge aus diesem kleinen Beispiel mit? Im Wesentlichen die folgenden Punkte:
- Computer benötigen eine exakt formulierte Befehlssequenz, um das zu erledigen, was wir von ihm erwarten – das Programm.
- Das Programm ist eine Umsetzung des allgemein formulierten Algorithmus in einer bestimmten Programmiersprache.
- Algorithmen bilden oft nur den Kern des Programms ab, nicht die ganze Funktionalität.
- Eine Planung der Vorgehensweise hilft, sich über die notwendigen Einzelheiten des Programms im Klaren zu sein.
- Während des Programmierprozesses treten oftmals neue, bis dato nicht in Betracht gezogene Problemstellungen zutage, welche kurzfristig gelöst werden müssen.
- Programme benötigen einen gewissen Overhead, damit sie überhaupt im eingesetzten System laufen. Dieser Overhead beinhaltet meist Standardstrukturen.
- Für Eingabe und Ausgabe, aber auch für weiterreichende Funktionen – in unserem Programm beispielsweise die Zufallsgenerierung – werden vorgefertigte Funktionalitäten genutzt, welche einfach aufgerufen werden können. Wir müssen diese dann nicht komplett selbst anfertigen.
So viel zum Einstieg in die Programmierwelt. Wir werden uns in den folgenden Kapiteln nun um die grundlegenden technischen
Einzelheiten kümmern, deren Verständnis eine zwingende Voraussetzung für das effiziente Programmieren ist. Dies mag jetzt
für den ein oder anderen etwas „trocken“ anmuten – wir wollen aber später nicht von irgendwelchen vermeintlich „merkwürdigen“
Verhaltensweisen des Computers überrascht werden!
Es werden in den nächsten Seiten diverse kleine Codeschnipsel gezeigt und besprochen. Natürlich kann jeder diesen Code
auf seinem eigenen Rechner ausprobieren. Da ich mich aber nicht auf eine bestimmte Programmiersprache festlegen möchte,
ist die Frage der Entwicklungsumgebung relativ schwierig. Für jede Programmiersprache gibt es sehr effektive und
angepasste Umgebungen. Bspw. wird Java gerne in IntelliJ oder Eclipse programmiert. Für PHP bietet sich NetBeans an, für
C# Visual Studio usw. Da vermutlich jetzt aber niemand für jede der hier gezeigten Programmiersprachen jeweils ein eigenes
Tool installieren möchte, gibt es eine recht gute Alternative, nämlich VS Code. Dieses Programm ist relativ
„leichtgewichtig“ – sprich es benötigt relativ wenige Ressourcen – es ist open Source und somit kostenlos und es läuft
auf Windows, iOS und Linux. Die online Beschreibungen für die Konfiguration zur Vorbereitung für die einzelnen
Programmiersprachen sind recht gut gestaltet und somit ist es ein guter Schritt für den Anfang. Sollte jemand sich dann für
größere Projekte für eine bestimmte Sprache entscheiden müssen, so kann man später immer noch eine angepasste Umgebung
für diesen Task auf seinem Rechner installieren. Ich habe den Installationsprozess für VS Code auf Windows im Kapitel
XX. VSCode kurz beschrieben, wobei die Onlinedokumentation unter
https://code.visualstudio.com/docs/ hier auch auf jeden Fall eine gute Quelle für Informationen bietet.

CC Lizenz (BY NC SA)
